题目内容
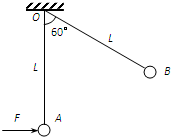 质量均为m的两个可视为质点的小球A、B,分别被长为L的绝缘细线悬挂在同一点O,给A、B分别带上一定量的正电荷,并用水平向右的外力作用在A球上,平衡以后,悬挂A球的细线竖直,悬挂B球的细线向右偏60°角,如图所示.若A球的带电量为q,则:
质量均为m的两个可视为质点的小球A、B,分别被长为L的绝缘细线悬挂在同一点O,给A、B分别带上一定量的正电荷,并用水平向右的外力作用在A球上,平衡以后,悬挂A球的细线竖直,悬挂B球的细线向右偏60°角,如图所示.若A球的带电量为q,则:(1)B球的带量为多少;
(2)水平外力多大.
分析:(1)对B球研究,分析受力情况,作出力图,由平衡条件求出库仑力,再由库仑定律求解B球的带量.
(2)对A球研究,分析受力情况,作出力图,由平衡条件求出水平外力.
(2)对A球研究,分析受力情况,作出力图,由平衡条件求出水平外力.
解答: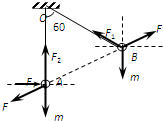 解:
解:
(1)当系统平衡以后,B球受到如图所示的三个力:重力mg、细线的拉力F1、库仑斥力F.由合力为零,由平衡条件得:
Fcos30°-F1cos30°=0
2Fsin30°-mg=0
由库仑定律:F=k
联立上述三式,可得B球的带电量qx=
(2)A球受到如图所示的四个力作用合力为零.
得 FT=F′?cos30°
而F′=F=k
所以,A球受到的水平推力FT=mgcos30°=
mg
答:(1)B球的带量为量qx=
;
(2)水平外力为=
mg.
 解:
解:(1)当系统平衡以后,B球受到如图所示的三个力:重力mg、细线的拉力F1、库仑斥力F.由合力为零,由平衡条件得:
Fcos30°-F1cos30°=0
2Fsin30°-mg=0
由库仑定律:F=k
| qqx |
| L2 |
联立上述三式,可得B球的带电量qx=
| mgL2 |
| kq |
(2)A球受到如图所示的四个力作用合力为零.
得 FT=F′?cos30°
而F′=F=k
| qqx |
| L2 |
所以,A球受到的水平推力FT=mgcos30°=
| ||
| 2 |
答:(1)B球的带量为量qx=
| mgL2 |
| kq |
(2)水平外力为=
| ||
| 2 |
点评:本题是简单的力平衡问题,考查选择研究对象,处理平衡问题的基本能力,采用的是隔离法.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
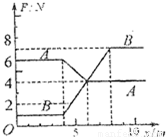
 水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是( )
水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是( )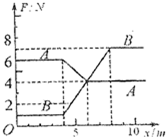 水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是
水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是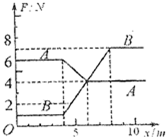
















 g
g
 。
。





