题目内容
【题目】如图所示，单匝正方形线框abcd质量M=0.3 kg、边长L=0.4 m、总电阻R=2 Ω。一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮，一端连接正方形线框另一端连接质量m=0.2 kg的物体P，线框释放前细线绷紧。在线框下方有一上下边界都水平的有界匀强磁场，两边界Ⅰ、Ⅱ之间距离h2=2 m，磁场方向水平且垂直纸面向里。现让线框cd边距上边界Ⅰ的高度h1=1 m处由静止释放，线框在运动过程中cd边始终保持水平且与磁场垂直，线框cd边进入磁场上边界Ⅰ时刚好做匀速运动，线框ab边刚进入磁场上边界Ⅰ时，线框上方的绝缘轻质细线突然断裂，不计空气阻力，求:
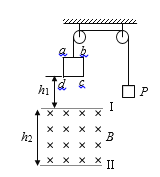
（1）线框cd边从磁场上边界Ⅰ进入时的速度大小v0
（2）匀强磁场的磁感应强度大小B
（3）线框穿过磁场过程中产生的焦耳热Q
【答案】v0=2 m/s；B=2.5 T；Q= 1.6 J
【解析】
（1）对线框与物体整体由动能定理：Mgh1﹣mgh1＝
（M+m）v02，代入数据解得：v0=2 m/s
（2）对物体P根据平衡条件有：T=mg ，同理对线框abcd：T+ILB=Mg，感应电动势：
，电流：
感应电流I= 
联立可得B=2.5 T
（3）线框匀速通过上边界Ⅰ过程中，根据功能关系有：Q1=ILB·L=0.4 J，线框ab进入磁场开始到cd边离开磁场过程中由动能定理：Mg(h2-L)= Mv2﹣Mv02 ，解得:v=6 m/s.，线框离开磁场过程中感应电流：:I1=
，安培力：F1=I1LB=3N，所以：Mg=F1 ，所以线框离开磁场过程中刚好做匀速运动线框离开磁场产生的焦耳热，根据功能关系有：Q2=MgL=1.2 J.所以产生的总热量：Q=Q1+Q2=1.6 J
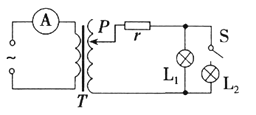
【题目】某实验小组的同学在学校实验室中发现一电学元件，该电学元件上标有“最大电流不超过6 mA，最大电压不超过7 V”，同学们想通过实验描绘出该电学元件的伏安特性曲线，他们设计的一部分电路如图所示，图中定值电阻R＝1 kΩ，用于限流；电流表量程为10 mA，内阻约为5 Ω；电压表(未画出)量程为10 V，内阻约为10 kΩ；电源电动势E为12 V，内阻不计，滑动变阻器阻值0～20 Ω，额定电流1 A。正确接线后，测得的数据如下表：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
U/V | 0.00 | 3.00 | 6.00 | 6.16 | 6.28 | 6.32 | 6.36 | 6.38 | 6.39 | 6.40 |
I/mA | 0.00 | 0.00 | 0.00 | 0.06 | 0.50 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 |
(1)由以上数据分析可知，电压表并联在M与________之间(填“O”或“P”)。
(2)将电路图在虚线框中补充完整_________。
(3)从表中数据可知，该电学元件的电阻特点是：________________________。
