题目内容
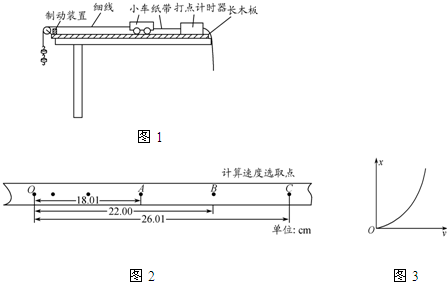
某实验小组采用如图1所示的装置来探究“功与速度变化的关系”.实验中,小车碰到制动装置时,钩码尚未到达地面.实验的部分步骤如下:
(1)将一块一端带有定滑轮的长木板固定在桌面上,在长木板的另一端固定打点计时器;
(2)把纸带穿过打点计时器的限位孔,连在小车后端,用细线跨过定滑轮连接小车和钩码;
(3)把小车拉到靠近打点计时器的位置,接通电源,从静止开始释放小车,得到一条纸带;
(4)关闭电源,通过分析小车位移与速度的变化关系来研究合外力对小车所做的功与速度变化的关系.
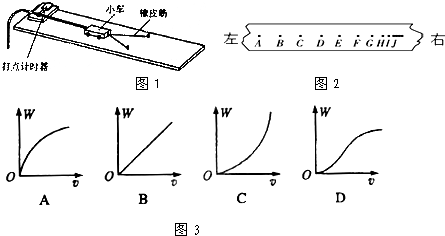
图2是实验中得到的一条纸带,点O为纸带上的起始点,A、B、C是纸带的三个计数点,相邻两个计数点间均有4个点未画出,用刻度尺测得A、B、C到O的距离如图所示,已知所用交变电源的频率为50Hz,问:
(1)打B点时刻,小车的瞬时速度vB=
(2)本实验中,若钩码下落高度为h1时合外力对小车所做的功W0,则当钩码下落h2时,合外力对小车所做的功为
w0
w0.(用h1、h2、w0表示)
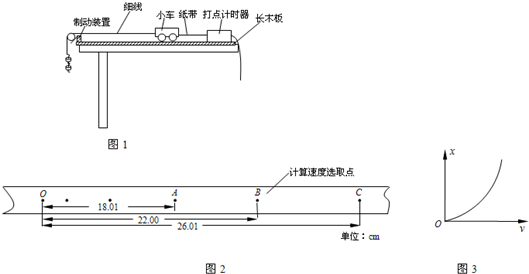
(3)实验中,该小组同学画出小车位移x与速度v的关系图象如图3所示.根据该图形状,某同学对W与v的关系作出的猜想,
肯定不正确的是
A.W∝v B.W∝v2
C.W∝
D.W∝v3
(4)在本实验中,下列做法能有效地减小实验误差的是
A.把长木板右端适当垫高,以平衡摩擦力
B.实验中控制钩码的质量,使其远小于小车的总质量
C.调节滑轮高度,使拉小车的细线和长木板平行
D.先让小车运动再接通打点计时器.

(1)将一块一端带有定滑轮的长木板固定在桌面上,在长木板的另一端固定打点计时器;
(2)把纸带穿过打点计时器的限位孔,连在小车后端,用细线跨过定滑轮连接小车和钩码;
(3)把小车拉到靠近打点计时器的位置,接通电源,从静止开始释放小车,得到一条纸带;
(4)关闭电源,通过分析小车位移与速度的变化关系来研究合外力对小车所做的功与速度变化的关系.
图2是实验中得到的一条纸带,点O为纸带上的起始点,A、B、C是纸带的三个计数点,相邻两个计数点间均有4个点未画出,用刻度尺测得A、B、C到O的距离如图所示,已知所用交变电源的频率为50Hz,问:
(1)打B点时刻,小车的瞬时速度vB=
0.40
0.40
m/s.(结果保留两位有效数字)(2)本实验中,若钩码下落高度为h1时合外力对小车所做的功W0,则当钩码下落h2时,合外力对小车所做的功为
| h2 |
| h1 |
| h2 |
| h1 |
(3)实验中,该小组同学画出小车位移x与速度v的关系图象如图3所示.根据该图形状,某同学对W与v的关系作出的猜想,
肯定不正确的是
AC
AC
(填写选项字母代号)A.W∝v B.W∝v2
C.W∝
| 1 |
| v |
(4)在本实验中,下列做法能有效地减小实验误差的是
ABC
ABC
(填写选项字母代号)A.把长木板右端适当垫高,以平衡摩擦力
B.实验中控制钩码的质量,使其远小于小车的总质量
C.调节滑轮高度,使拉小车的细线和长木板平行
D.先让小车运动再接通打点计时器.
分析:(1)根据匀变速直线运动的平均速度等于中间时刻瞬时速度求解B点速度.
(2)根据功的定义W=FS?COSα求解.
(3)根据图象为过原点的曲线,结合数学函数知识分析.
(2)根据功的定义W=FS?COSα求解.
(3)根据图象为过原点的曲线,结合数学函数知识分析.
解答:解:(1)匀变速直线运动的平均速度等于中间时刻瞬时速度,故
vB=
=
m/s=0.40m/s
(2)根据功的定义,有
W0=mgh1
W=mgh2
解得
W=
w0
(3)图象为过原点的曲线,故W与v一定不是正比关系,也一定不是反比关系.故选AC
(4)本实验探究“功与速度变化的关系”的实验,要使钩码的重力等于小车的合外力,就必须先平衡摩擦力,保证钩码的质量远小于小车的总质量,所以AB都正确,调节滑轮高度,使拉小车的细线和长木板平行,让力的方向和位移方向在同一直线上,可以减小误差,故C正确,应该先接通电源,后放开小车,所以D错误,故选C.
故答案为:(1)0.40;(2)
w0;(3)AC;(4)ABC.
vB=
| xAC |
| 2T |
| 0.2601-0.1801 |
| 0.2 |
(2)根据功的定义,有
W0=mgh1
W=mgh2
解得
W=
| h2 |
| h1 |
(3)图象为过原点的曲线,故W与v一定不是正比关系,也一定不是反比关系.故选AC
(4)本实验探究“功与速度变化的关系”的实验,要使钩码的重力等于小车的合外力,就必须先平衡摩擦力,保证钩码的质量远小于小车的总质量,所以AB都正确,调节滑轮高度,使拉小车的细线和长木板平行,让力的方向和位移方向在同一直线上,可以减小误差,故C正确,应该先接通电源,后放开小车,所以D错误,故选C.
故答案为:(1)0.40;(2)
| h2 |
| h1 |
点评:本题重点考查了“探究功与动能变化关系”实验的原理,以及数据处理方法,解题时从实验原理角度分析即可.

练习册系列答案
相关题目