题目内容
如图所示,宽度为L的平行光滑的金属轨道,左端为半径为r1的四分之一圆弧轨道,右端为半径为r2的半圆轨道,中部为与它们相切的水平轨道.水平轨道所在的区域有磁感应强度为B的竖直向上的匀强磁场.一根质量为m的金属杆a置于水平轨道上,另一根质量为M的金属杆b由静止开始自左端轨道最高点滑下,当b滑入水平轨道某位置时,a就滑上了右端半圆轨道最高点(b始终运动且a、b未相撞),并且a在最高点对轨道的压力大小为mg,此过程中通过a的电荷量为q,a、b棒的电阻分别为R1、R2,其余部分电阻不计.在b由静止释放到a运动到右端半圆轨道最高点过程中,求:
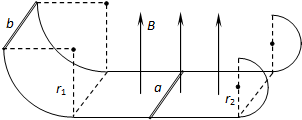 (1)在水平轨道上运动时b的最大加速度是多大?
(1)在水平轨道上运动时b的最大加速度是多大?
(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是多少?
(3)a刚到达右端半圆轨道最低点时b的速度是多大?
 (1)在水平轨道上运动时b的最大加速度是多大?
(1)在水平轨道上运动时b的最大加速度是多大?(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是多少?
(3)a刚到达右端半圆轨道最低点时b的速度是多大?
分析:(1)b棒从左侧轨道下滑的过程中,只有重力做功,其机械能守恒,求出b进入刚进入水平轨道时的速度大小.进入水平轨道后b棒切割磁感线产生感应电流,a棒由于受到安培力作用向右运动,回路中产生的感应电动势将要减小,感应电流也减小,则知b棒的加速度减小,则b棒刚进入磁场时加速度最大,由牛顿第二定律和安培力公式结合求解.
(2)此过程中通过a的电荷量为q,根据动量定理求出b棒后来的速度.对a棒:由牛顿运动定律求出通过最高点时的速度,由机械能守恒定律求出离开磁场时的速度.由能量守恒定律即可求解系统产生的焦耳热.
(3)当两棒都在水平轨道上运动时,两棒组成的系统合外力为零,动量守恒,可求出a刚到达右端半圆轨道最低点时b的速度.
(2)此过程中通过a的电荷量为q,根据动量定理求出b棒后来的速度.对a棒:由牛顿运动定律求出通过最高点时的速度,由机械能守恒定律求出离开磁场时的速度.由能量守恒定律即可求解系统产生的焦耳热.
(3)当两棒都在水平轨道上运动时,两棒组成的系统合外力为零,动量守恒,可求出a刚到达右端半圆轨道最低点时b的速度.
解答:解:(1)b棒从左侧轨道下滑的过程,由机械能守恒定律:
M
=Mgr1
∴vb1=
b刚滑到水平轨道时加速度最大,
由E=BLvb1,I=
,F安=BIL=Ma得
∴a=
(2)根据动量定理得-BILt=Mvb2-Mvb1
又It=q,即-BLq=Mvb2-Mvb1
∴vb2=
-
对a棒,在根据牛顿第三定律得:N=N′=mg
在轨道最高点:mg+N=m
∴va1=
根据能量守恒定律得:
Mgr1=
M
+
m
+mg2r2+Q
得Q=
BLq-3mgr2-
(3)∵2mgr2=
m
-
m
∴va2=
当两棒都在水平轨道上运动时,两棒组成的系统合外力为零,动量守恒,则有
Mvb1=Mvb3+mva2
∴vb3=
-
答:
(1)在水平轨道上运动时b的最大加速度是
.
(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是
BLq-3mgr2-
.
(3)a刚到达右端半圆轨道最低点时b的速度是
-
.
| 1 |
| 2 |
| v | 2 b1 |
∴vb1=
| 2gr1 |
b刚滑到水平轨道时加速度最大,
由E=BLvb1,I=
| E |
| R1+R2 |
∴a=
B2L2
| ||
| M(R1+R2) |
(2)根据动量定理得-BILt=Mvb2-Mvb1
又It=q,即-BLq=Mvb2-Mvb1
∴vb2=
| 2gr1 |
| BLq |
| M |
对a棒,在根据牛顿第三定律得:N=N′=mg
在轨道最高点:mg+N=m
| ||
| r2 |
∴va1=
| 2gr2 |
根据能量守恒定律得:
Mgr1=
| 1 |
| 2 |
| v | 2 b2 |
| 1 |
| 2 |
| v | 2 a1 |
得Q=
| 2gr1 |
| B2L2q2 |
| 2M |
(3)∵2mgr2=
| 1 |
| 2 |
| v | 2 a2 |
| 1 |
| 2 |
| v | 2 a1 |
∴va2=
| 6gr2 |
当两棒都在水平轨道上运动时,两棒组成的系统合外力为零,动量守恒,则有
Mvb1=Mvb3+mva2
∴vb3=
| 2gr1 |
| m |
| M |
| 6gr2 |
答:
(1)在水平轨道上运动时b的最大加速度是
B2L2
| ||
| M(R1+R2) |
(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是
| 2gr1 |
| B2L2q2 |
| 2M |
(3)a刚到达右端半圆轨道最低点时b的速度是
| 2gr1 |
| m |
| M |
| 6gr2 |
点评:本题是“双杆”类型,两棒都在水平轨道上运动的过程类似于碰撞,基本规律是动量守恒和能量守恒,本题综合性较强.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
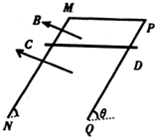 如图所示,宽度为L的足够长的平行金属导轨MN、PQ的电阻不计,垂直导轨水平放置一质量为m电阻为R的金属杆CD,整个装置处于垂直于导轨平面的匀强磁场中,导轨平面与水平面之间的夹角为θ,金属杆由静止开始下滑,动摩擦因数为μ,下滑过程中重力的最大功率为P,求磁感应强度的大小.
如图所示,宽度为L的足够长的平行金属导轨MN、PQ的电阻不计,垂直导轨水平放置一质量为m电阻为R的金属杆CD,整个装置处于垂直于导轨平面的匀强磁场中,导轨平面与水平面之间的夹角为θ,金属杆由静止开始下滑,动摩擦因数为μ,下滑过程中重力的最大功率为P,求磁感应强度的大小.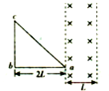 如图所示,宽度为L的有界匀强磁场的方向垂直纸面向里,磁感应强度的大小为B.闭合等腰直角三角形导线框abc的直角边ab长为2L.线框总电阻为R.规定沿abca方向为感应电流的正方向.导线框以速度v匀速向右穿过磁场的过程中,感应电流随时间变化规律的图象是( )
如图所示,宽度为L的有界匀强磁场的方向垂直纸面向里,磁感应强度的大小为B.闭合等腰直角三角形导线框abc的直角边ab长为2L.线框总电阻为R.规定沿abca方向为感应电流的正方向.导线框以速度v匀速向右穿过磁场的过程中,感应电流随时间变化规律的图象是( )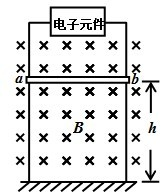 如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k为恒量.框架上有一质量为m的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h,磁感应强度为B的匀强磁场与框架平面相垂直.将金属棒由静止释放,棒沿框架向下运动.不计金属棒电阻,问:
如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k为恒量.框架上有一质量为m的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h,磁感应强度为B的匀强磁场与框架平面相垂直.将金属棒由静止释放,棒沿框架向下运动.不计金属棒电阻,问: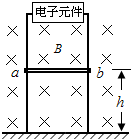 (2012?盐城三模)如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一个电子元件,其阻值与其两端所加的电压成正比,即R=kU,式中k为常数.框架上有一质量为m,离地高为h的金属棒,金属棒与框架始终接触良好无摩擦,且保持水平.磁感应强度为B的匀强磁场方向垂直于框架平面向里.将金属棒由静止释放,棒沿框架向下运动,不计金属棒电阻.重力加速度为g.求:
(2012?盐城三模)如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一个电子元件,其阻值与其两端所加的电压成正比,即R=kU,式中k为常数.框架上有一质量为m,离地高为h的金属棒,金属棒与框架始终接触良好无摩擦,且保持水平.磁感应强度为B的匀强磁场方向垂直于框架平面向里.将金属棒由静止释放,棒沿框架向下运动,不计金属棒电阻.重力加速度为g.求: