题目内容
如图所示,斜面的倾角为θ=37o,物块m1和m2之间用轻绳相连,m1=m2=1kg,斜面与m1之间的动摩擦因数为μ=0.25,m2离地面高度h=8m,系统由静止开始运动,假设斜面和轻绳足够长,求:(取g=10m/s2,sin37o=0.6,cos37°=0.8)
(1)m2在落地前瞬间速度多大?
(2)当m2落地后,m1还能向上滑行多远? 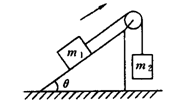
(1)4m/s(2)1m
解析试题分析:(1)以m1、m2组成的系统为研究对象,由牛顿第二定律可得:
m2g―m1gsinθ―μm1gcosθ=(m1+m2)a
则:a=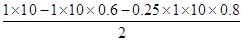 =1m/s2
=1m/s2
设m2落地时速度大小为v1,则:
v1=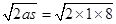 =4m/s
=4m/s
(2)m2落地后,m1沿斜面向上做匀减速运动,由牛顿第二定律可得:
m1gsinθ+μm1gcosθ=m1a'
则: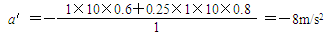
则m1还可滑行的距离为:
s=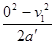 =
=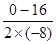 =1m
=1m
考点:牛顿第二定律;
点评:本题是连接体问题,涉及两个过程.此题也可以根据动能定理,分两个过程求解.

某小组“验证牛顿第二定律”的实验装置如下图,长木板固定在水平桌面上,一端装有定滑轮;木板上有一滑块,其一端与电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接。
(1)该小组研究加速度和拉力关系时,得到的图象将会是图 
(2)下图给出的是实验中获取的一条纸带的一部分:1、2、3、4、5、6、7是计数点每相邻两计数点间还有4个打点(图中未标出),计数点间的距离如图所示。根据图中数据计算的加速度a= m/s2(保留三位有效数字)。
(3)某同学在研究加速度和质量关系时,记录下如下数据,请在下面的坐标纸中选择合理的坐标,描出相关图线,并可以由图线可以得到实验结论: 。
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 质量m/g | 200 | 300 | 400 | 500 | 600 |
| 加速度a/m˙s-2 | 1.00 | 0.67 | 0.50 | 0.40 | 0.33 |

甲、乙两队参加拔河比赛,甲队胜,若不计绳子的质量,下列说法正确的是( )
| A.甲队拉绳子的力大于乙队拉绳子的力 |
| B.甲队对地面的摩擦力大于乙队对地面的摩擦力 |
| C.甲、乙两队与地面间的最大静摩擦力大小相等、方向相反 |
| D.甲、乙两队拉绳子的力大小相等 |
用牛顿第三定律判断下列说法正确的是( )
| A.轮船的螺旋桨旋转时,向后推水,水同时给螺旋桨一个反作用力,推动轮船前进 |
| B.发射火箭时,燃料点燃后喷出的气体给空气一个作用力,推动火箭前进 |
| C.马拉车前进,只有马对车的拉力大于车对马的拉力时,车才能前进 |
| D.一个作用力和它的反作用力的合力为零 |
如图所示,质量一定的汽车驶过圆弧形桥面顶点时未脱离桥面,关于汽车所处的运动状态以及对桥面的压力,以下说法正确的是 ( )
| A.汽车处于超重状态,它对桥面的压力大于汽车的重力 |
| B.汽车处于超重状态,它对桥面的压力小于汽车的重力 |
| C.汽车处于失重状态,它对桥面的压力大于汽车的重力 |
| D.汽车处于失重状态,它对桥面的压力小于汽车的重力 |
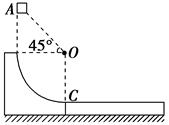
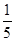 ,g取10 m/s2,求:
,g取10 m/s2,求: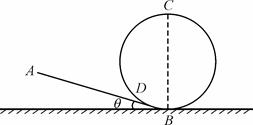

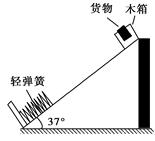
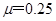 .设计要求:木箱在轨道顶端时,自动装货装置将质量
.设计要求:木箱在轨道顶端时,自动装货装置将质量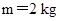 的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取
的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取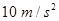 ,sin 37°=0.6 ,cos 37°=0.8.求:
,sin 37°=0.6 ,cos 37°=0.8.求: