��Ŀ����
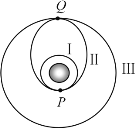
����Ŀ����ͼ��ʾ����Եˮƽ���ڹ̶���һ���d=lm�����費�Ƶ��㹻���⻬���ε���AKDC���������˽�����ֵ�ֱ�ΪR1=3����R2=6���Ķ�ֵ����.��������AKFE��NMCD��Χ�ھ��з�����ֱ���¡��Ÿ�Ӧǿ�ȴ�СB=1T����ǿ�ų�I������һ����m=0.2kg������r=1���ĵ����ab��ֱ���ڵ�����AK��EF֮��ij�����ڷ���ˮƽ���ҡ���СF0=2N�ĺ����������ɾ�ֹ��ʼ�˶����յ���EFʱ�����ab���ٶȴ�Сv1=3m��s�������ab����ų��������ab��ͨ���ĵ���ʼ�ձ��ֲ��䡣�����ab���˶�������ʼ�ձ����뵼�촹ֱ�ҽӴ����ã������������ơ�������
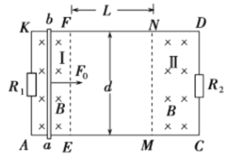
A.�����ab�յ���EFʱ�ļ��ٶȴ�СΪ5m/s2
B.���ų��߽�EF��MN֮��ľ���LΪ1m
C.���ڵ����ab�յ���MNʱ��������ȥ�������ab�������еľ���Ϊ3m
D.���ڵ����ab�յ���MNʱ��������ȥ�������ab�������еĹ�����������·�����Ľ�����Ϊ3.6J
���𰸡�AD
��������
A�������ab��Ҫ����EFʱ���ڴų����и�Ÿ��߲����ĸ�Ӧ�綯��
E1=Bdv1
��������֪����ʱ�����ab���ܰ������ķ���ˮƽ������ţ�ٵڶ����ɣ�����
F0-BI1d=ma1
���ݱպϵ�·��ŷķ���ɣ�����
![]()
��ʽ��
![]()
���
a1=5m/s2
ѡ��A��ȷ��
B�������ab����ų�����ܵ��İ�������F0ƽ�⣬������ֱ���˶��������ab��ͨ���ĵ���I2�����ֲ��䣬����
F0=BI2d
����
![]()
�赼���ab��EF�˶���MN�Ĺ����еļ��ٶȴ�СΪa2������ţ�ٵڶ����ɣ�����
F0=ma2
�����ab��EF��MN֮�����ȼ���ֱ���˶�������
![]()
���
L=1.35m
ѡ��B����
C���Գ�ȥF0�����ab�������еĹ����У�����ţ�ٵڶ����ɺͱպϵ�·ŷķ���ɣ�����
BId=ma
��
![]()
����t��0������
![]()
��������ʽ�ɵ�
![]()
����
![]()
��
![]()
���
s=3.6m
ѡ��C����
D�����������غ㶨�ɣ�����
![]()
��v2=6m/s���������ݽ��
Q=3.6J
ѡ��D��ȷ��
��ѡAD��