题目内容
（14分）如图所示，OAB是刚性轻质直角三角形支架，边长AB=20cm，∠OAB=30°；在三角形两锐角处分别固定两个不计大小的小球，A处小球质量为1kg。现将支架安装在可自由转动的水平轴上，使之可绕O点在竖直平面内无摩擦转动。装置静止时，AB边恰好水平。求：
（1）B处小球的质量；
（2）若将装置顺时针转动30°，至少需做多少功；
（3）若将装置顺时针转动30°后由静止释放，支架转动的最大角速度。
（1）B处小球的质量；
（2）若将装置顺时针转动30°，至少需做多少功；
（3）若将装置顺时针转动30°后由静止释放，支架转动的最大角速度。
（1）3kg（2）2
–3（3）
–3（3）试题分析：（1）mAgAOcos30°=mBgBOsin30° 2分
mB=mAcot230°=3kg 2分
（2）W=mAgAO sin30°- mBgBO（1- cos30°） 2=2
–3 (J) 2分（3）在平衡位置，物体的势能最小，动能最大，支架转动的角速度最大 2分
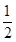mA(ωAO)2+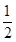mB(ωBO)2= mAgAO sin30°- mBgBO（1- cos30°） 2分ω=
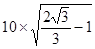rad/s ="3.93" rad/s点评：本题的关键是把握装置运动过程中的特殊状态，如在平衡位置是，势能最小，动能最大，角速度最大，根据动能定理分析解题
练习册系列答案
相关题目
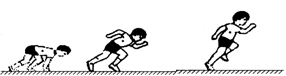
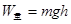
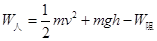
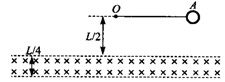
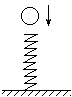
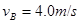飞出后，恰好能从一倾角为
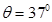的倾斜传送带顶端C无碰撞的滑上传送带，已知传送带长度为L=2.75m（图中只画出了传送带的部分示意图）物体与传送带之间的动摩擦因数为
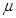=0.50，（取sin370=0.60，cos370=0.80，g=10m/s2不计空气阻力，不考虑半圆形管AB的内径）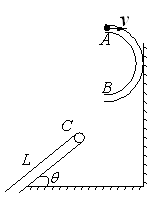
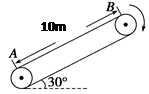
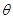=30°,其上A、B两点间的距离为L="10" m,传送带在电动机的带动下以v="5" m/s的速度匀速运动,现将一质量为m="10" kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数
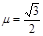,在传送带将小物体从A点传送到B点的过程中,求:（g=10m/s2）
