题目内容
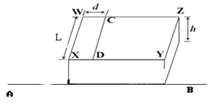
【题目】如图所示,正方形光滑水平台面WXYZ边长L=1.8m,距地面高h=0.8m。CD线平行于WX边,且它们间距d=0.1m。一个质量为m的微粒从W点静止释放,在WXDC平台区域受到一个从W点指向C点的恒力F1=1.25×10-11N作用,进入CDYZ平台区域后,F1消失,受到另一个力F2作用,其大小满足F2=5×10-13v(v是其速度大小),运动过程中其方向总是垂直于速度方向,从而在平台上做匀速圆周运动,然后由XY边界离开台面,(台面以外区域F2=0)。微粒均视为质点,取g=10m/s2。
(1)若微粒质量m=1×10-13kg,求微粒在CDYZ平台区域运动时的轨道半径;
(2)若微粒质量m=1×10-13kg,求微粒落地点到平台下边线AB的距离。
【答案】(1)1m;(2)1.2m
【解析】
(1)微粒从W到C,由牛顿第二定律得
![]()
又
![]()
所以
![]()
微粒在CDYZ区域运动时,![]() 提供向心力,由牛顿第二定律得
提供向心力,由牛顿第二定律得
![]()
得
![]()
(2)微粒在CDYZ区域运动时,其运行轨迹如图
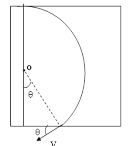
由几何关系得
![]()
![]()
微粒离开平台后做平抛运动
![]()
![]()
所以
![]()
故微粒落地点到平台下边线AB的距离为
![]()

练习册系列答案
相关题目