题目内容
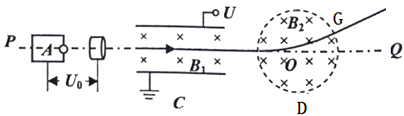
【题目】如图，在x轴上方存在匀强磁场，磁感应强度大小为B，方向垂直于纸面向外；在x轴下方存在匀强电场，电场方向与xOy平面平行，且与x轴成45°夹角．一质量为m、电荷量为q（q＞0）的粒子以速度v0从y轴上P点沿y轴正方向射出，一段时间后进入电场，进入电场时的速度方向与电场方向相反；又经过一段时间T0 ， 磁场方向变为垂直纸面向里，大小不变，不计重力．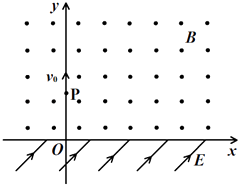
（1）求粒子从P点出发至第一次到达x轴时所需的时间；
（2）若要使粒子能够回到P点，求电场强度的最大值．
【答案】
（1）
解：带电粒子在磁场中做圆周运动，设运动半径为R，运动周期为T，
洛伦兹力提供向心力，由牛顿第二定律得： 
，
粒子做圆周运动的周期： 
，
由题意可知，粒子第一次到达x轴时，运动转过的角度为 
，
所需时间t1为： 
，解得： 
；
（2）
解：粒子进入电场后，先做匀减速运动，直到速度减小为0，
然后沿原路返回做匀加速运动，到达x轴时速度大小仍为v0，
设粒子在电场中运动的总时间为t2，加速度大小为a，电场强度大小为E，
由牛顿第二定律得：qE=ma， 
，解得： 
，
根据题意，要使粒子能够回到P点，必须满足t2≥T0，
解得，电场强度最大值： 
．
【解析】（1）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律与粒子的周期公式求出粒子的运动时间．（2）分析清楚粒子在电场中的运动过程，应用牛顿第二定律、运动学公式求出电场强度．
练习册系列答案
全优点练单元计划系列答案
相关题目
