题目内容
7.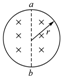 如图所示,在一半径为r的圆形区域内有垂直向里的匀强磁场,磁感应强度为B,ab为一直径,在磁场的边界上b点处放置一个粒子源,可以向磁场内的各个方向发射质量均为m和电量均为q(q>0)的粒子,粒子进入磁场的速度大小均相同,发现圆形磁场边界上有六分之一的区域有粒子射出.则下列说法正确的是( )
如图所示,在一半径为r的圆形区域内有垂直向里的匀强磁场,磁感应强度为B,ab为一直径,在磁场的边界上b点处放置一个粒子源,可以向磁场内的各个方向发射质量均为m和电量均为q(q>0)的粒子,粒子进入磁场的速度大小均相同,发现圆形磁场边界上有六分之一的区域有粒子射出.则下列说法正确的是( )| A. | 进入到磁场中的粒子的速度大小为$\frac{qBr}{m}$ | |
| B. | 进入到磁场中的粒子的速度大小为$\frac{qBr}{2m}$ | |
| C. | 若将离子源发射的粒子速度变为原来的二倍,则磁场边界上有一半区域有粒子射出 | |
| D. | 若将离子源发射的粒子速度变为原来的二倍,则磁场边界上所有区域均有粒子射出 |
分析 离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据题意求出离子转过的最大圆心角,然后应用几何知识求出离子的轨道半径,再应用牛顿第二定律求出离子的速度,然后答题.
解答 解:A、从b点射入的粒子与磁场边界的最远交点为c,最远的点是轨迹上直径与磁场边界圆的交点,相应的弧长变为圆周长的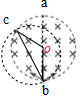 $\frac{1}{6}$,所以∠bOc=60°;
$\frac{1}{6}$,所以∠bOc=60°;
由几何关系可知,粒子的轨道半径:R=$\frac{1}{2}$r…①,
粒子在磁场中做匀速圆周运动,仑兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{R}$…②
联立①②解得:v=$\frac{qBr}{2m}$,故A错误,B正确;
C、若将离子源发射的粒子速度变为原来的二倍,则粒子在磁场中做圆周运动的轨道半径:R′=$\frac{mv′}{qB}$=$\frac{2mv}{qB}$=2×$\frac{1}{2}$r=r,则粒子转过的最大圆心角∠bOc=90°,离子射出的圆弧为圆形磁场区域的一半,即磁场边界上有一半区域有粒子射出,即C正确,D错误;
故选:B,C.
点评 带电粒子在电磁场中的运动一般有直线运动、圆周运动和一般的曲线运动;直线运动一般由动力学公式求解,圆周运动由洛仑兹力充当向心力,一般的曲线运动一般由动能定理求解;本题关键画出临界轨迹.

练习册系列答案
相关题目
12.下列说法符合史实的是( )
| A. | 开普勒发现了万有引力定律 | |
| B. | 牛顿提出了日心说 | |
| C. | 卡文迪许第一次在实验室里测出了万有引力常量 | |
| D. | 哥白尼提出了地心说 |
10.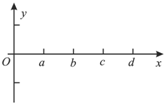 如图所示,O是波源,a、b、c、d是波传播方向上四个质点的平衡位置,且oa=ab=bc=cd,t1=0时各质点均静止在平衡位置,波源O开始沿y轴正方向做简谐运动,形成一列沿x轴正方向传播的简谐波.在t2=0.3s,波源O第一次到达负向最大位移处,简谐波恰好传到c点.下列说法正确的是( )
如图所示,O是波源,a、b、c、d是波传播方向上四个质点的平衡位置,且oa=ab=bc=cd,t1=0时各质点均静止在平衡位置,波源O开始沿y轴正方向做简谐运动,形成一列沿x轴正方向传播的简谐波.在t2=0.3s,波源O第一次到达负向最大位移处,简谐波恰好传到c点.下列说法正确的是( )
 如图所示,O是波源,a、b、c、d是波传播方向上四个质点的平衡位置,且oa=ab=bc=cd,t1=0时各质点均静止在平衡位置,波源O开始沿y轴正方向做简谐运动,形成一列沿x轴正方向传播的简谐波.在t2=0.3s,波源O第一次到达负向最大位移处,简谐波恰好传到c点.下列说法正确的是( )
如图所示,O是波源,a、b、c、d是波传播方向上四个质点的平衡位置,且oa=ab=bc=cd,t1=0时各质点均静止在平衡位置,波源O开始沿y轴正方向做简谐运动,形成一列沿x轴正方向传播的简谐波.在t2=0.3s,波源O第一次到达负向最大位移处,简谐波恰好传到c点.下列说法正确的是( )| A. | 波的周期为1.2s | |
| B. | t2=0.3s,a质点向y轴正方向运动 | |
| C. | t2=0.3s,b质点的加速度达正向最大 | |
| D. | 当d点开始振动时的起振方向沿y轴正方向 |
19.矩形线圈在匀强磁场中匀速转动产生的电动势e-t图象如图,则( )
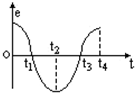

| A. | t1、t3时刻线圈通过中性面时刻 | |
| B. | t2、t4时刻线圈中磁通量最大 | |
| C. | t1、t3时刻线圈中磁通量变化率最大 | |
| D. | t2、t4时刻线圈平面与中性面垂直 |
17.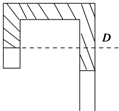 竖直倒立的U形玻璃管一端封闭,另一端开口向下,如图所示,用水银柱封闭一定质量的理想气体,在保持温度不变的情况下,假设在管子的D处钻一小孔,则管内被封闭的气体压强p和气体体积V变化的情况为( )
竖直倒立的U形玻璃管一端封闭,另一端开口向下,如图所示,用水银柱封闭一定质量的理想气体,在保持温度不变的情况下,假设在管子的D处钻一小孔,则管内被封闭的气体压强p和气体体积V变化的情况为( )
 竖直倒立的U形玻璃管一端封闭,另一端开口向下,如图所示,用水银柱封闭一定质量的理想气体,在保持温度不变的情况下,假设在管子的D处钻一小孔,则管内被封闭的气体压强p和气体体积V变化的情况为( )
竖直倒立的U形玻璃管一端封闭,另一端开口向下,如图所示,用水银柱封闭一定质量的理想气体,在保持温度不变的情况下,假设在管子的D处钻一小孔,则管内被封闭的气体压强p和气体体积V变化的情况为( )| A. | p、V都不变 | B. | V增大,p减小 | C. | V减小,p增大 | D. | 无法确定 |

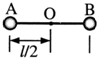 如图所示,在水平向右的匀强电场中,长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为3m和5m,A带负电,电量为q,B带正电,电量也为q.若杆在水平位置,由静止开始转动,杆能转过的最大角度为53°,则匀强电场的场强E=$\frac{2mg}{q}$;在转动过程,则AB两球组成的系统的电势能的改变量为0.8mgL.
如图所示,在水平向右的匀强电场中,长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为3m和5m,A带负电,电量为q,B带正电,电量也为q.若杆在水平位置,由静止开始转动,杆能转过的最大角度为53°,则匀强电场的场强E=$\frac{2mg}{q}$;在转动过程,则AB两球组成的系统的电势能的改变量为0.8mgL.