题目内容
18. 通过探究得到弹性势能的表达式为Ep=$\frac{1}{2}$kx2,式中k为弹簧的劲度系数,x为弹簧伸长(或缩短)的长度.请利用弹性势能的表达式计算下列问题:
通过探究得到弹性势能的表达式为Ep=$\frac{1}{2}$kx2,式中k为弹簧的劲度系数,x为弹簧伸长(或缩短)的长度.请利用弹性势能的表达式计算下列问题:放在地面上的物体上端系在劲度系数k=200N/m的弹簧上,弹簧的另一端拴在跨过定滑轮的绳子上,如图所示.手拉右侧绳子的另一端,当拉力往下做功为4J时,物体开始离开地面,继续拉绳再做功32J,使物体缓慢升高到离地一定高度处,如果不计弹簧重和滑轮跟绳的摩擦,求:
(1)弹簧的弹性势能;
(2)右侧绳端总共下降的高度.
分析 (1)弹簧的弹性势能等于F做的功.
(2)根据Ep=$\frac{1}{2}$kx2,求出弹簧伸长的长度.物体开始离开地面时F=mg,根据物体上升的高度和弹簧伸长量之和求右侧绳端总共下降的高度.
解答 解:(1)弹簧的弹性势能为:Ep=WF=4J
(2)由Ep=$\frac{1}{2}$kx2得:x=0.2m
物体离地后:W2=Fh=mgh
而mgh=kx
联立得:h=0.8m
综上,右侧绳端总共下降的高度为:h总=x+h=1m
答:(1)弹簧的弹性势能是4J;
(2)右侧绳端总共下降的高度是1m.
点评 能够通过问题情境分析找出一些条件,分清绳端的位移和弹簧长度的关系,难度不大.

练习册系列答案
相关题目
9.一个质点沿直线运动,初速度大小为2m/s,末速度大小为4m/s,则( )
| A. | 速度的改变量的大小可能是6 m/s | |
| B. | 速度的改变量的大小可能是4 m/s | |
| C. | 速度改变量的方向可能与初速度的方向相同 | |
| D. | 速度改变量的方向可能与初速度的方向相反 |
6.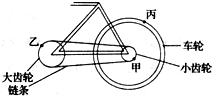 自行车传动系统的示意图如图所示,小齿轮、大齿轮和车轮的半径分别为r1、r2、r3,它们的边缘上有三个点甲、乙、丙,其中哪些点的向心加速度之间的关系适用于“向心加速度跟半径成反比”( )
自行车传动系统的示意图如图所示,小齿轮、大齿轮和车轮的半径分别为r1、r2、r3,它们的边缘上有三个点甲、乙、丙,其中哪些点的向心加速度之间的关系适用于“向心加速度跟半径成反比”( )
 自行车传动系统的示意图如图所示,小齿轮、大齿轮和车轮的半径分别为r1、r2、r3,它们的边缘上有三个点甲、乙、丙,其中哪些点的向心加速度之间的关系适用于“向心加速度跟半径成反比”( )
自行车传动系统的示意图如图所示,小齿轮、大齿轮和车轮的半径分别为r1、r2、r3,它们的边缘上有三个点甲、乙、丙,其中哪些点的向心加速度之间的关系适用于“向心加速度跟半径成反比”( )| A. | 甲、乙 | B. | 乙、丙 | C. | 甲、丙 | D. | 甲、乙、丙 |
13. 在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到vm后立即关闭发动机直到停止,其v-t图象如图所示.设汽车牵引力F的做功为W1,克服摩擦力f做的功为W2,则( )
在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到vm后立即关闭发动机直到停止,其v-t图象如图所示.设汽车牵引力F的做功为W1,克服摩擦力f做的功为W2,则( )
 在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到vm后立即关闭发动机直到停止,其v-t图象如图所示.设汽车牵引力F的做功为W1,克服摩擦力f做的功为W2,则( )
在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到vm后立即关闭发动机直到停止,其v-t图象如图所示.设汽车牵引力F的做功为W1,克服摩擦力f做的功为W2,则( )| A. | F:f=1:2 | B. | F:f=3:1 | C. | W1:W2=1:1 | D. | W1:W2=1:3 |
3.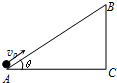 如图所示,长为L,倾斜为θ的光滑绝缘斜面处于电场中.一带电量为+q,质量为m 的小球,以初速度vO由斜面底端的A 点开始沿斜面上滑,到达斜面顶端的速度仍为vO,则( )
如图所示,长为L,倾斜为θ的光滑绝缘斜面处于电场中.一带电量为+q,质量为m 的小球,以初速度vO由斜面底端的A 点开始沿斜面上滑,到达斜面顶端的速度仍为vO,则( )
 如图所示,长为L,倾斜为θ的光滑绝缘斜面处于电场中.一带电量为+q,质量为m 的小球,以初速度vO由斜面底端的A 点开始沿斜面上滑,到达斜面顶端的速度仍为vO,则( )
如图所示,长为L,倾斜为θ的光滑绝缘斜面处于电场中.一带电量为+q,质量为m 的小球,以初速度vO由斜面底端的A 点开始沿斜面上滑,到达斜面顶端的速度仍为vO,则( )| A. | 小球在B 点的电势能一定大于小球在A 点的电势能 | |
| B. | A、B两点的电势差一定为 $\frac{mgL}{q}$ | |
| C. | 若电场是匀强电场,则该电场的场强的最小值一定是 $\frac{mgsinθ}{q}$ | |
| D. | 运动过程中小球所受重力与电场力必相等 |
10.做简谐运动的物体,全振动30次用了24s,则它的周期和频率分别为( )
| A. | 0.8s,1.25Hz | B. | 1.25s,0.8Hz | C. | 1.6s,2.5Hz | D. | 2.5s,1.6Hz |
7.火车在平直轨道上匀速前进,在密封的没有空气滑动的车厢内点燃了一支卫生香,则车里的乘客看到卫生香所冒的烟的运动情况是( )
| A. | 一边上升一边向前飘 | B. | 一边上升一边向后飘 | ||
| C. | 只是上升不向任何一边飘 | D. | 无法确定 |
8.如图所示,一细棒质量为m,初始时θ=30°,方形木块以恒定速度向正左方运动,则细棒受到木块的力( )
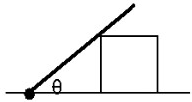

| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
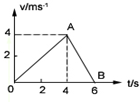 某物体作直线运动的速度-时间图象如图所示,根据图象回答:
某物体作直线运动的速度-时间图象如图所示,根据图象回答: