题目内容
19. 如图所示,AB为两水平放置的平行金属板,两板间距为d,分别与电源两极相连,两板的中央各有一小孔M和N.让一带电质点自P点(P与M间的距离为d)由静止自由下落(P、M、N在同一竖直线上),结果到达N孔时速度恰好为零.然后沿原路返回,空气阻力忽略不计.重力加速度为g.
如图所示,AB为两水平放置的平行金属板,两板间距为d,分别与电源两极相连,两板的中央各有一小孔M和N.让一带电质点自P点(P与M间的距离为d)由静止自由下落(P、M、N在同一竖直线上),结果到达N孔时速度恰好为零.然后沿原路返回,空气阻力忽略不计.重力加速度为g.(1)保持两极板间的电势差不变,把A板向下平移一小段距离△d,质点自P点自由下落后能否穿过N孔继续下落?若能,求质点到达N孔时速度的大小.
(2)保持两极板间的电势差不变,把B板向下平移一小段距离△d,质点自P点自由下落后能否穿过N孔继续下落?若能,求质点到达N孔时速度的大小.
分析 根据动能定理分别分析A板不动时和移动时,质点到达N板孔的速度,判断质点能否穿过N孔.
解答 解:(1)设电容器两板间的电压为U,由题质点到达N孔时速度恰好为零,根据动能定理得:2mgd-qU=0 ①
下把A板向上平移一小段距离,由于板间电压U不变,质点从P到达N过程,电场力做功仍为-qU,不变,重力做功为2mgd,不变,则根据动能定理分析得知,质点到达N孔的速度为零.则质点自P点下落仍从N点返回.
(2)B板向下平移的距离为△d,质点到达N点的速度为v,根据动能定理得
mg(2d+△d)-qU=$\frac{1}{2}m{v}^{2}$②
联立①②得到,v=$\sqrt{2g△d}$>0,则质点自P点下落后从N孔穿出并继续下落.
答:(1)保持两极板间的电势差不变,把A板向下平移一小段距离△d,质点自P点自由下落后不能穿过N孔继续下落;
(2)保持两极板间的电势差不变,把B板向下平移一小段距离△d,质点自P点自由下落后能穿过N孔继续下落,质点到达N孔时速度的大小是$\sqrt{2g△d}$.
点评 本题运用动能定理分析质点的运动情况,抓住电场力做W=-qU保持不变是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
20.物体做匀加速直线运动,加速度为2m/s2,那么( )
| A. | 在任意时间内,物体的末速度一定等于初速度的2倍 | |
| B. | 在任意时间内,物体的末速度一定比初速度大于2m/s | |
| C. | 在任意1s内,物体的末速度一定等于初速度的2倍 | |
| D. | 在任意1s内,物体的末速度一定比初速度大2m/s |
14.在验证机械能守恒定律的实验中,要验证的是重锤重力势能的减少量等于它的动能的增加,以下步骤中仅是实验中的一部分,在这些步骤中多余的或错误的有( )
| A. | 把打点计时器固定在铁架台上,并用导线把它和低压直流电源连接起来 | |
| B. | 把纸带的一端固定在重锤上,另一端穿过打点计时器的限位孔,把重锤提升到一定的高度 | |
| C. | 接通电源,释放纸带 | |
| D. | 用秒表测出重锤下落的时间 |
11.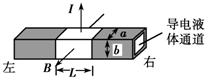 电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )
电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )
 电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )
电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )| A. | 导电液体可能向左流动 | B. | 导电液体一定向右流动 | ||
| C. | 电磁泵的功率为$\frac{{B}^{2}ab{I}^{2}}{k}$ | D. | 电磁泵的功率为$\frac{{B}^{2}{b}^{2}{I}^{2}}{k}$ |
8. 如图所示,在竖直平面内放一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直.一个带正电荷的小滑块由静止开始从半圆轨道的最高点M滑下,则下列说法中正确的是( )
如图所示,在竖直平面内放一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直.一个带正电荷的小滑块由静止开始从半圆轨道的最高点M滑下,则下列说法中正确的是( )
 如图所示,在竖直平面内放一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直.一个带正电荷的小滑块由静止开始从半圆轨道的最高点M滑下,则下列说法中正确的是( )
如图所示,在竖直平面内放一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直.一个带正电荷的小滑块由静止开始从半圆轨道的最高点M滑下,则下列说法中正确的是( )| A. | 滑块经过最低点时的速度与磁场不存在时要大 | |
| B. | 滑块从M点滑到最低点所用的时间与磁场不存在时相等 | |
| C. | 滑块经过最低点时的加速度比磁场不存在时要大 | |
| D. | 滑块经过最低点时对轨道的压力与磁场不存在时相等 |
9.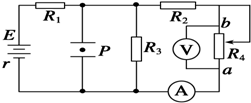 如图所示,平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则( )
如图所示,平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则( )
 如图所示,平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则( )
如图所示,平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则( )| A. | 电压表读数减小 | B. | 电流表读数减小 | ||
| C. | 质点P将向上运动 | D. | R1上消耗的功率逐渐增大 |
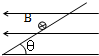
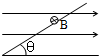
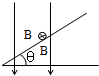
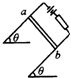 质量为m的通电细杆ab置于倾角为θ的平行导轨上,导轨宽为d,ab与导轨间的摩擦因数为μ,有电流时ab恰好在导轨上静止,如图所示,是沿ba方向观察时的四个平面图,标出了四种不同的匀强磁场方向,其中杆与导轨间摩擦力可能为零的是( )
质量为m的通电细杆ab置于倾角为θ的平行导轨上,导轨宽为d,ab与导轨间的摩擦因数为μ,有电流时ab恰好在导轨上静止,如图所示,是沿ba方向观察时的四个平面图,标出了四种不同的匀强磁场方向,其中杆与导轨间摩擦力可能为零的是( )