题目内容
【题目】如图所示,将一个质量为1kg的小球用细线悬挂起来,线长0.9m.现将小球拉至使细线与竖直方向成60°角的位置,然后由静止释放,不计空气阻力,求: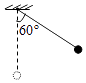
(1)小球运动到最低位置时的速度大小;
(2)小球运动到最低位置时对细线的拉力.
【答案】
(1)解:小球下摆过程只有重力做功,故机械能守恒,根据机械能守恒定律可知:
mgL(1﹣cos60°)= ![]()
解得:v=3m/s
答:小球运动到最低位置时的速度大小是3m/s;
(2)解:小球在最低位置时受到的拉力和重力的合力提供向心力,则
T﹣mg=m ![]()
解得:T=20N
根据牛顿第三定律可知小球运动到最低点时对细线的拉力大小为20N.
答:小球运动到最低位置时对细线的拉力是20N.
【解析】(1)小球在向下摆动的过程中只有重力做功,机械能守恒,由机械能守恒定律可求小球运动到最低点时的速度大小;(2)小球运动到最低位置时,由合力提供向心力,由牛顿第二定律求细线对小球的拉力大小.
【考点精析】根据题目的已知条件,利用机械能守恒及其条件的相关知识可以得到问题的答案,需要掌握在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变.

练习册系列答案
相关题目