Question

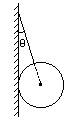
用绳将球A挂在光滑竖直墙上，如图所示．（1）现施加外力矩将球A绕球心顺时针转过一个小角度，外力矩撤去后，球的运动情况如何？（2）若墙面不光滑，情况又如何？（3）墙面光滑，绳子变短时，绳的拉力和球对墙的压力将如何变化？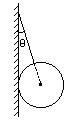

Answer 1

答案：见详解
解析：

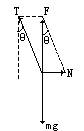
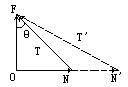
（1）因为墙是光滑的，绳子的作用力一定过球心．取球为研究对象，受力图如图1所示．N为墙对球的力，方向水平向右；重力mg方向竖直向下；绳拉力T沿绳的方向，θ为绳与墙的夹角．因为小球静止，所以N、T、mg的合力为零，即T、N的合力F大小等于mg，方向竖直向上，T=mg/cosθ，N=mgtanθ． 当球A受到外力矩使其顺时针转动一个小角度后，重力mg和墙对球的支持力方向不变且均过球心，而绳对球A的作用力T不再过球心，且此力T对球A中心产生一使球A逆时针转动的力矩，墙面光滑无摩擦力．所以外力矩撤去后，球A在力T对球A的力矩作用下使球A绕球心逆时针转动．当球A转动到原平衡位置时，球A具有转动动能而继续转动，转动到一定角度后速度为零，而后球A向顺时针方向转动，再次转动到平衡位置时，球A仍具有转动动能而继续顺时针方向转动，转动为零后又重复上述过程． （2）若墙不光滑，球A的受力情况就比较复杂，若开始时球A如图所示，则墙与球A接触点无相对滑动的趋势，球A不受静摩擦力的作用，当球A受到外力矩使球A顺时针绕球心转过一个小角度时，若墙和球A之间的静摩擦系数足够大，球A在外力矩撤去后仍可静止不动，若顺时针转动的角度过大，运动情况与（1）讨论中类似，但最后在何处静止取决于系统的初始状态及系统本身，过程过于复杂这里不再讨论． （3）研究变量的问题，我们要紧紧抓住被研究变量与不变量之间的关系，这是研究此类问题的一般思路和方法．由图可知： 图1 T=mg/cosθ　　　　　　　　　　　　　　　　　　　　　　　　　　 ① N=mgtanθ　　　　　　　　　　　　　　　　　　　　　　　　　　 ② 墙面光滑，当绳子变短时，θ角增大，式①中cosθ将变小，但其在分母上故整个分式变大，即T增大；式②中tanθ随θ变大而增大，故N也增大． 此题也可用图解法求解，因为T、N的合力F大小为mg，方向竖直向上，N的方向也已知总是垂直于墙（这些都是不变的量）．即已知合力和一个分力的方向求另一个分力．根据矢量合成的三角形法则，由图2可知，当θ增大时，N变为N′，T变为T′，都将增大． 图2

提示：

考查力矩和受力分析。