题目内容
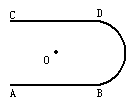
如图所示,半径为R的光滑绝缘圆环固定在竖直平面内,在环的底端B点固定一个带正电的小球,环上还套有一个质量为m,带等量正电荷的小球,现将小球从A点(半径OA水平)由静止释放开始运动,当运动到C点(∠AOC= )时获得的最大动能为Ekm,求:
)时获得的最大动能为Ekm,求:

(1)小球从位置A运动到位置C的过程中所受静电力做的功W;
(2)小球在A点刚释放时运动的加速度a;
(3)小球在位置C时受到圆环对它的作用力.
 )时获得的最大动能为Ekm,求:
)时获得的最大动能为Ekm,求:
(1)小球从位置A运动到位置C的过程中所受静电力做的功W;
(2)小球在A点刚释放时运动的加速度a;
(3)小球在位置C时受到圆环对它的作用力.
(1)Ekm-
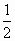 mgR. (2)(1-
mgR. (2)(1-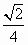 )g (3) mg+2Ekm/R.
)g (3) mg+2Ekm/R. (1)由A→C根据动能定理m gRsin +
+ =Ekm,
=Ekm,
得 =Ekm-
=Ekm-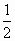 mgR.
mgR.
(2)由C点受力平衡,可判定mg= ,
,
又∵ 无穷趋近于
无穷趋近于 ,∴
,∴ =
=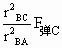 =
=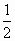 mg.
mg.
又∵vA=0,∴a=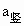 =(mg-
=(mg- cos
cos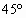 )/m
)/m
=(1-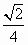 )g.
)g.
(3)在C点 与mg的合力恰好为mg,方向沿OC.
与mg的合力恰好为mg,方向沿OC.
N-mg=mv2/R,得N=mg+2Ekm/R.
 +
+ =Ekm,
=Ekm,得
 =Ekm-
=Ekm-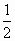 mgR.
mgR.(2)由C点受力平衡,可判定mg=
 ,
,又∵
 无穷趋近于
无穷趋近于 ,∴
,∴ =
=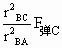 =
=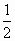 mg.
mg.又∵vA=0,∴a=
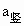 =(mg-
=(mg- cos
cos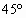 )/m
)/m=(1-
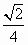 )g.
)g.(3)在C点
 与mg的合力恰好为mg,方向沿OC.
与mg的合力恰好为mg,方向沿OC.N-mg=mv2/R,得N=mg+2Ekm/R.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目

 向B球运动,此时B球速度为零,设两球始终没相碰,求它们之间的最短距离是多少?
向B球运动,此时B球速度为零,设两球始终没相碰,求它们之间的最短距离是多少?

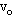 按如图所示的方向射入木刚好能将木块射穿.现在拔去销钉,使木块能在水平面上自由滑动,而子弹仍以速度
按如图所示的方向射入木刚好能将木块射穿.现在拔去销钉,使木块能在水平面上自由滑动,而子弹仍以速度
 高处的B点停止.若在B点给物体一瞬时冲量,使物体从B点沿着原路返回到A点,需要给物体的最小冲量值是多大?
高处的B点停止.若在B点给物体一瞬时冲量,使物体从B点沿着原路返回到A点,需要给物体的最小冲量值是多大?