题目内容
原长为L0的轻弹簧一端固定一小铁块,另一端连接在竖直轴OO′上,小铁块放在水平圆盘上,若圆盘静止,把弹簧拉长后将小铁块放在圆桌上,弹簧的最大长度为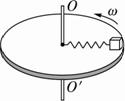
图
解析:以小铁块为研究对象,受到四个力的作用.在竖直方向上,铁块的重力与圆盘对铁块的支持力相互抵消;在水平方向,铁块受到的摩擦力f与弹簧的拉力kx提供向心力.
由牛顿第二定律得:kx±f=m(![]() L0)ω2
L0)ω2
要使ω达最大,±f中应取“+”号,且f→fm,则根据题意
fm=kL0/4,x=![]() L0代入得:
L0代入得:
![]() kL0+
kL0+![]() kL0=m(
kL0=m(![]() L0)ω2,
L0)ω2,
则角速度的最大值ω=![]() .
.
答案:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
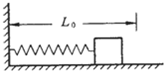
 如图所示,在水平桌面上推物体压缩一个原长为L0的轻弹簧.桌面与物体之间有摩擦,放手后物体被弹簧弹开,则( )
如图所示,在水平桌面上推物体压缩一个原长为L0的轻弹簧.桌面与物体之间有摩擦,放手后物体被弹簧弹开,则( ) 如图所示,一劲度系数为k、原长为l0的轻弹簧,上端固定在天花板上,下端悬挂一个质量为m的小球,小球处于静止状态.弹簧的形变在 弹性限度内.已知重力加速度为g.下列判断正确的是( )
如图所示,一劲度系数为k、原长为l0的轻弹簧,上端固定在天花板上,下端悬挂一个质量为m的小球,小球处于静止状态.弹簧的形变在 弹性限度内.已知重力加速度为g.下列判断正确的是( )