题目内容
8. 如图所示,空间中存在一水平方向匀强电场和一水平方向匀强磁场,且电场方向和磁场方向相互垂直.在电磁场正交的空间中有一足够长的固定粗糙绝缘杆,与电场正方向成60°夹角且处于竖直平面内.一质量为m,带电量为+q的小球套在绝缘杆上.初始,给小球一沿杆向下的初速度v0,小球恰好做匀速运动,电量保持不变.已知,磁感应强度大小为B,电场强度大小为E=$\frac{\sqrt{3}mg}{q}$,则以下说法正确的是( )
如图所示,空间中存在一水平方向匀强电场和一水平方向匀强磁场,且电场方向和磁场方向相互垂直.在电磁场正交的空间中有一足够长的固定粗糙绝缘杆,与电场正方向成60°夹角且处于竖直平面内.一质量为m,带电量为+q的小球套在绝缘杆上.初始,给小球一沿杆向下的初速度v0,小球恰好做匀速运动,电量保持不变.已知,磁感应强度大小为B,电场强度大小为E=$\frac{\sqrt{3}mg}{q}$,则以下说法正确的是( )| A. | 小球的初速度为v0=$\frac{2mg}{qB}$ | |
| B. | 若小球的初速度为$\frac{3mg}{qB}$,小球将做加速度不断增大的减速运动,最后停止 | |
| C. | 若小球的初速度为$\frac{mg}{qB}$,小球将做加速度不断增大的减速运动,最后停止 | |
| D. | 若小球的初速度为$\frac{mg}{qB}$,则运动中克服摩擦力做功为$\frac{3{m}^{3}{g}^{2}}{2{q}^{2}{B}^{2}}$ |
分析 小球受重力、摩擦力(可能有)、弹力(可能有)、向右上方的洛伦兹力、向左的电场力,当受到的合外力等于0时,小球做匀速直线运动.当小球受到的合外力不为0时,要判断出支持力的方向,明确支持力的大小随洛伦兹力的变化关系,然后做出判定.
解答 解:A、对小球进行受力分析如图,
电场力的大小:F=qE=$q×\frac{\sqrt{3}mg}{q}=\sqrt{3}mg$,由于重力的方向竖直向下.电场力的方向水平向右,二者垂直,合力:${F}_{G+F}=\sqrt{{F}^{2}+(mg)^{2}}=2mg$,由几何关系可知,重力与电场力的合力与杆的方向垂直,所以重力与电场力的合力不会对小球做功,而洛伦兹力的方向与速度的方向垂直,所以也不会对小球做功.所以,当小球做匀速直线运动时,不可能存在摩擦力,没有摩擦力,说明小球与杆之间就没有支持力的作用,则洛伦兹力大小与重力、电场力的合力相等,方向相反.所以qv0B=2mg.
所以v0=$\frac{2mg}{qB}$.故A正确;
B、若小球的初速度为$\frac{3mg}{qB}$,则洛伦兹力:f=qv0B=3mg>FG+F,则在垂直于杆的方向上,小球还受到杆的垂直于杆向下的支持力,则摩擦力:f=μFN.小球将做减速运动;随速度的减小,洛伦兹力减小,则支持力逐渐减小,摩擦力减小,小球做加速度不断减小的减速运动,最后当速度减小到$\frac{2mg}{qB}$时,小球开始做匀速直线运动.故B错误.
C、若小球的初速度为$\frac{mg}{qB}$,则洛伦兹力:f=qv0B=mg<FG+F,则在垂直于杆的方向上,小球还受到杆的垂直于杆向上的支持力,而摩擦力:f=μFN.小球将做减速运动;随速度的减小,洛伦兹力减小,则支持力逐渐增大,摩擦力逐渐增大,小球的加速度增大,所以小球将做加速度不断增大的减速运动,最后停止.故C正确;
D、若小球的初速度为$\frac{mg}{qB}$,球将做加速度不断增大的减速运动,最后停止,运动中克服摩擦力做功等于小球的动能,所以W=$\frac{1}{2}m{v}_{0}^{2}$=$\frac{{m}^{3}{g}^{2}}{2{q}^{2}{B}^{2}}$.故D错误.
故选:AC
点评 本题考查小球在混合场中的运动,解答的关键明确小球的受力情况,并能够结合受力的情况分析小球的运动情况,要知道小球何时做加速度减小的减速运动,何时做加速度增大的减速运动,当加速度减为零时,做匀速运动.

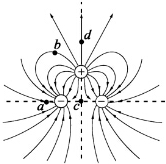 两个相同的负电荷和一个正电荷附近的电场线分布如图所示,c是两负电荷连线的中点,d点在正电荷的正上方,c、d到正电荷的距离相等,则( )
两个相同的负电荷和一个正电荷附近的电场线分布如图所示,c是两负电荷连线的中点,d点在正电荷的正上方,c、d到正电荷的距离相等,则( )| A. | a点的电场强度比b点的大 | B. | a点的电势比b点的高 | ||
| C. | c点的电场强度比d点的大 | D. | c点的电势比d点的低 |

| A. | 在O点右侧杆上,B点场强最大,场强大小为E=1.2V/m | |
| B. | 由C到A的过程中,小球的电势能先减小后变大 | |
| C. | 沿着C到A的方向,电势先降低后升高 | |
| D. | C、B两点间的电势差UCB=1.0V |
| A. | 相对论和量子力学的出现说明人类对自然界的认识更加广泛和深入,那么经典力学就失去了它的意义 | |
| B. | 交流感应电动机就是利用电磁阻尼的原理工作的 | |
| C. | 地磁场在北半球的上空有垂直于地表向上的磁场分量 | |
| D. | 电流通过纯电阻电路做功时,电能全部转化为该电路的内能 |
| A. | X粒子为α粒子 | |
| B. | X粒子的动量与反冲核的动量大小相等 | |
| C. | 该粒子与阴极射线的组成成分相同 | |
| D. | 反冲核的中子数为136 | |
| E. | 该粒子与反冲核的速率之比为1:43 |
 如图,小车静止在光滑水平地面上,小车的上表面由光滑斜面AB和粗糙水平面BC组成(它们在B处由极短的光滑圆弧平滑连接),小车右侧与竖直墙壁之间连接着一个力传感器,当传感器受压力时,其示数为正值,当传感器受拉力时,其示数为负值.一小滑块(可视为质点)从A点由静止开始下滑,经B向C点运动的过程中力传感器记录了力F随时间t变化的关系,该关系在下面四个图象中可能正确的是( )
如图,小车静止在光滑水平地面上,小车的上表面由光滑斜面AB和粗糙水平面BC组成(它们在B处由极短的光滑圆弧平滑连接),小车右侧与竖直墙壁之间连接着一个力传感器,当传感器受压力时,其示数为正值,当传感器受拉力时,其示数为负值.一小滑块(可视为质点)从A点由静止开始下滑,经B向C点运动的过程中力传感器记录了力F随时间t变化的关系,该关系在下面四个图象中可能正确的是( )



 如图所示,等腰三角形OPQ区域内存在场强方向沿PQ方向、大小为E的匀强电场,A为PQ的中点,D为OQ的中点,PQ=2L,θ=30°.一质量为m、电量为 q的带正电粒子(重力不计、初速度视为零),从靠近M板O′处由静止释放,经两平行金属板M、N间的电场加速后,通过N板上的小孔沿AO方向从A点射入三角形OPQ区域,粒子恰好从D点射出电场.
如图所示,等腰三角形OPQ区域内存在场强方向沿PQ方向、大小为E的匀强电场,A为PQ的中点,D为OQ的中点,PQ=2L,θ=30°.一质量为m、电量为 q的带正电粒子(重力不计、初速度视为零),从靠近M板O′处由静止释放,经两平行金属板M、N间的电场加速后,通过N板上的小孔沿AO方向从A点射入三角形OPQ区域,粒子恰好从D点射出电场.
 质谱仪可以测定有机化合物分子结构,其结构如图所示.有机物分子从样品室注入“离子化”室,在高能电子作用下,样品分子离子化或碎裂成离子(如C2H6离子化后得到C2H6+、CH4+等).若这些离子均带一个单位的正电荷e,且初速度为零.此后经过高压电源区、圆形磁场室、真空管,最后在记录仪上得到离子.已知高压电源的电压为U,圆形磁场区的半径为R,真空管与水平线夹角为θ,离子沿半径方向飞入磁场室,且只有沿真空细管轴线进入的离子才能被记录仪记录.
质谱仪可以测定有机化合物分子结构,其结构如图所示.有机物分子从样品室注入“离子化”室,在高能电子作用下,样品分子离子化或碎裂成离子(如C2H6离子化后得到C2H6+、CH4+等).若这些离子均带一个单位的正电荷e,且初速度为零.此后经过高压电源区、圆形磁场室、真空管,最后在记录仪上得到离子.已知高压电源的电压为U,圆形磁场区的半径为R,真空管与水平线夹角为θ,离子沿半径方向飞入磁场室,且只有沿真空细管轴线进入的离子才能被记录仪记录.