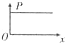题目内容
 如图所示,边长为L、电阻为R的正方形刚性导体线圈abcd,水平地放置在磁感应强度为B的斜向上的匀强磁场中,磁场方向与水平的夹角为37°,磁场区域足够大.现以线圈的ad边为轴使线圈以不变的角速度?逆时针旋转90°角,求:
如图所示,边长为L、电阻为R的正方形刚性导体线圈abcd,水平地放置在磁感应强度为B的斜向上的匀强磁场中,磁场方向与水平的夹角为37°,磁场区域足够大.现以线圈的ad边为轴使线圈以不变的角速度?逆时针旋转90°角,求:(1)指出此过程感应电流的方向,并求出感应电动势的平均值.
(2)此过程通过线圈横截面的电荷量.
(3)此过程中bc边受到的安培力的最大值.
分析:(1)根据楞次定律,可确定感应电流的方向;由法拉第电磁感应定律,可求出平均感应电动势的大小;
(2)根据电量表达式,与感应电动势的大小相结合,即可求解;
(3)由线圈切割磁感线产生最大感应电动势的表达式,与闭合电路欧姆定律,及安培力的表达式,即可求解.
(2)根据电量表达式,与感应电动势的大小相结合,即可求解;
(3)由线圈切割磁感线产生最大感应电动势的表达式,与闭合电路欧姆定律,及安培力的表达式,即可求解.
解答:解:(1)根据楞次定律,则有感应电流方向:abcda.
线圈逆时针旋转90°过程,磁通量变化量所用时间:△t=
,
而磁通量的变化量:△?=Bcos37?L2+Bsin37°?L2=
此过程平均感应电动势:
=
=
=
(2)通过线圈横截面的电荷量:Q=
?△t=
?△t=
=
(3)当线圈平面与磁感线平行,感应电流最大,bc边所受的安培力也最大.
则有:Em=BL?Lω=BL2ω
由闭合电路欧姆定律,则有:Im=
=
bc边所受的最大安培力:则有:Fm=BImL=
答:(1)指出此过程感应电流的方向:abcda,且感应电动势的平均值
.
(2)此过程通过线圈横截面的电荷量
.
(3)此过程中bc边受到的安培力的最大值
.
线圈逆时针旋转90°过程,磁通量变化量所用时间:△t=
| π |
| 2ω |
而磁通量的变化量:△?=Bcos37?L2+Bsin37°?L2=
| 7BL2 |
| 5 |
此过程平均感应电动势:
. |
| E |
| △? |
| △t |
| ||
|
| 14BωL2 |
| 5π |
(2)通过线圈横截面的电荷量:Q=
. |
| I |
| ||
| R |
| △? |
| R |
| 7BL2 |
| 5R |
(3)当线圈平面与磁感线平行,感应电流最大,bc边所受的安培力也最大.
则有:Em=BL?Lω=BL2ω
由闭合电路欧姆定律,则有:Im=
| Em |
| R |
| BL2ω |
| R |
bc边所受的最大安培力:则有:Fm=BImL=
| B2L3ω |
| R |
答:(1)指出此过程感应电流的方向:abcda,且感应电动势的平均值
| 14BωL2 |
| 5π |
(2)此过程通过线圈横截面的电荷量
| 7BL2 |
| 5R |
(3)此过程中bc边受到的安培力的最大值
| B2L3ω |
| R |
点评:考查楞次定律、法拉第电磁感应定律的应用,掌握左手定则与右手定则的区别,注意求电量的通项式:Q=N
,并掌握安培力大小计算.
| △? |
| R |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,边长为L的正方形区域abcd内存在着匀强电场.电荷量为q、动能为Ek的带电粒子从a点沿ab方向垂直于电场线进入电场,不计重力作用
如图所示,边长为L的正方形区域abcd内存在着匀强电场.电荷量为q、动能为Ek的带电粒子从a点沿ab方向垂直于电场线进入电场,不计重力作用 一质点从如图所示的边长为L的正方形轨道的一个顶点开始沿轨道做匀速率运动,质点运动速率为v,在运动过程中:
一质点从如图所示的边长为L的正方形轨道的一个顶点开始沿轨道做匀速率运动,质点运动速率为v,在运动过程中: 如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )
如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( ) 如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.若粒子从c点离开电场,则电场强度的大小为
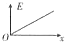
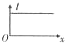
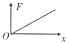
如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.若粒子从c点离开电场,则电场强度的大小为 如图所示,边长为L的正三角形闭合金属框架,全部处于垂直于框架平面的匀强磁场中,现把框架匀速拉出磁场,图象中E为回路电动势,I为回路电流,F为所加外力,P为回路电功率,x为框架位移.则框架拉出磁场的过程中,正确的图象是( )
如图所示,边长为L的正三角形闭合金属框架,全部处于垂直于框架平面的匀强磁场中,现把框架匀速拉出磁场,图象中E为回路电动势,I为回路电流,F为所加外力,P为回路电功率,x为框架位移.则框架拉出磁场的过程中,正确的图象是( )