题目内容
如图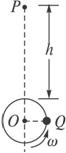
图
解析:小球Q在竖直平面内做匀速圆周运动具有重复性特点,要求小球P在距圆周最高点为h处开始自由下落至在圆周最高点处相碰,则在小球P下落时间内小球Q转过(n+![]() )圈,即小球P下落时间是小球Q匀速圆周运动的(n+
)圈,即小球P下落时间是小球Q匀速圆周运动的(n+![]() )倍.由此切入列方程即可求解.
)倍.由此切入列方程即可求解.
自由落体的位移公式h=![]() gt2,可求得小球P自由下落运动至圆周最高点的时间为t1=
gt2,可求得小球P自由下落运动至圆周最高点的时间为t1=![]() ①
①
设小球Q做匀速圆周运动的周期为T,则有T=![]() ②
②
由题意知,球Q由图示位置运动至圆周最高点所用时间为t2=(n+![]() )T ③
)T ③
(n=0,1,2…)
要使两球在圆周最高点相碰,需使t1=t2 ④
以上四式联立,解得球Q做匀速圆周运动的角速度为ω=π(4n+1)![]()
(n=0,1,2…),
即要使两球在圆周最高点处相碰,Q球的角速度ω应满足
ω=π(4n+1)![]() (n=0,1,2…).
(n=0,1,2…).

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目