题目内容

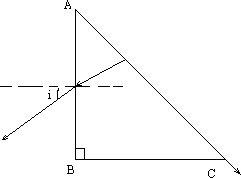
如图所示，用某种折射率较大的透光物质制成的直角三棱镜ABC，已知∠BAC=90°，∠ABC=30°．在垂直于AC面的直线MN上插上两枚大头针P1、P2，在AB面的左侧通过棱镜观察大头针P1、P2的像，调整视线方向，直到P1的像被P2的像挡住，在观察的这一侧先后插上两枚大头针P3、P4，使P3挡住
P2
P2
的像，使P4挡住
P3
P3
和
P2
P2
的像，记下P3、P4和棱镜的位置，移去大头针和三棱镜，过P3、P4作直线与AB面交于D，量出该直线与AB间的夹角为45°，则该物质的折射率n=
2
2
，并作出光路图标出D的位置．
分析：用插针法测定玻璃砖折射率的原理是的折射定律n=
sini
sinr
．其方法是：在AB面的左侧透过棱镜观察大头针P1、P2的像，调整视线方向，直到P1的像被P2的像挡住，再在观察的这一侧先后插上两枚大头针P3、P4，使P3挡住P1、P2，P4挡住P1、P2以及P3的像．连接P1、P2作为入射光线，连接P3、P4，作为出射光线，再作出折射光线，由折射定律求解折射率．
解答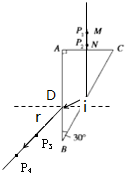：解：在AB面的左侧透过棱镜观察大头针P1、P2的像，调整视线方向，直到P1的像被P2的像挡住，再在观察的这一侧先后插上两枚大头针P3、P4，使P3挡住P1、P2，P4挡住P1、P2以及P3的像．则知P1、P2在入射光线上，P3、P4在出射光线，连接P1、P2作为入射光线，连接P3、P4，作为出射光线，再作出折射光线，如图．
由几何知识得到入射角i=30°，又折射角r=45°，则折射率n=
sinr
sini
=
2
．
画出光路图如图．
故答案为：P2，P3，P2，
2
点评：本题要理解实验的原理：折射定律n=
sini
sinr
，懂得如何确定出射光线．本题中光线CB面上发生了全反射．
练习册系列答案
相关题目
（1）在“测定玻璃的折射率”的实验中，选用的是入射面和出射面相互平行的矩形玻璃砖，用“插针法”测定某种玻璃的折射率．实验步骤如下：
a．将木板水平放置，把一张白纸用图钉固定在木板上；
b．在白纸上画出一条直线aa’作为入射界面，过aa’上的一点O画出界面的法线NN’，并画一条线段AO作为入射光线；
c．把矩形玻璃砖放在白纸上，使它的长边跟aa’对齐，画出玻璃砖的另一边bb’；
d．在直线AO上竖直插上两枚大头针P1、P2，透过玻璃砖观察大头针P1、P2的像，调整视线方向，直到P2档住P1的像．再在观察的这一侧插两枚大头针P3、P4，
使P3挡住P1、P2的像，P4挡住P3及P1、P2的像
使P3挡住P1、P2的像，P4挡住P3及P1、P2的像
，记下P3、P4的位置．
e．移去大头针和玻璃砖，做出出射光线，标出入射角α、折射角β．
①请将步骤d补充完整．
②小明同学按上述步骤进行了实验，记录下5组数据，并计算出不同入射角时玻璃的折射率，如下表所示．
组别
项目		 第1组 第2组 第3组 第4组 第5组
入射角α 25° 35° 45° 50° 75°
折射角β 16° 22.5° 28° 32° 42°
sinα 0.423 0.574 0.707 0.766 0.966
sin β 0.276 0.383 0.469 0.530 0.669
折射率n 1.533 1.499 1.506 1.446 1.443
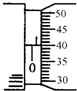但其中有一组数据是不真实的，李老师给出了该玻璃砖的折射率为n=1.521，arcsin(
1
1.521
)=0.717（弧度）=41.081°．根据老师给出的数据可以判断，小明同学记录的数据中，不真实的是第
5
5
组．
③赵亮同学在找到入射光线和折射光线以后，以入射点O为圆心，以任意长为半径画圆，分别与AO交于C点，与OOˊ交于D点，过C、D两点分别向NNˊ作垂线，交NNˊ于Cˊ、Dˊ，所以折射率n=
CC′
DD′
CC′
DD′
．（用图示中的线段表示）
（2）在“测定金属的电阻率”的实验中，提供的器材除螺旋测微器、米尺、开关和若干导线外，还有：
待测粗细均匀的金属丝Rx （阻值约为10Ω）
直流电流表：A1（量程100mA，内阻为2Ω）
A2（量程400mA，内阻约为0.3Ω）
直流电压表：V1（量程4V，内阻约为3kΩ）
V2（量程15V，内阻约为12kΩ）
滑动变阻器：R （阻值范围0～10Ω）
电源：E （电动势为3V，内阻约为0.04Ω）
①实验时，用螺旋测微器在金属丝三个不同的位置测直径，某次测量的情况如图所示，其读数为
0.900
0.900
mm．
②某同学选择如图（甲）所示的电路图测该金属丝的电阻，为了调节方便，测量准确，实验中应选用电流表
A2
A2
，电压表
V1
V1
．（填器材的符号）
③选择了正确的器材后，请你根据电路图（甲），用笔画线代替导线，在实物图（乙）上连线．
④若电压表、电流表读数用U、I表示，导线的长度为L，直径为d，用上述测得的物理量计算金属丝的电阻率的表示式为ρ=
πUd2
4IL
πUd2
4IL
．
某位同学用下面的方法测量某种液体的折射率．如图所示，他在一个烧杯中装满了某种透明液体，紧贴着杯口竖直插入一根直尺AB，眼睛从容器边缘的P处斜向下看去，观察到A经液面反射所成的虚像A′恰好与B经液体折射形成的虚像重合．他读出直尺露出液面的长度AC、没入液体中的长度BC，量出烧杯的直径d．由此求出这种透明液体的折射率为（　　）
（2008?昆明模拟）如图所示，A、B、C为等腰棱镜，a、b两束不同频率的单色光垂直AB边射入棱镜，折射后两束光相交于图中的P点，以下判断正确的是（　　）
（2011?泗阳县一模） （选做题）本题包括A、B、C三小题，请选定其中两题，并在相应答题区域内作答．若三题都做，则按A、B两题评分．
A．（选修3-3模块）
（1）以下说法中正确的是
A．物体内能取决于温度、体积和物质的量
B．布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映
C．浸润和不浸润均是分子力作用的表现
D．液晶对不同颜色光的吸收强度随电场强度的变化而变化
（2）如图所示，气缸内封闭一定质量的某种理想气体，活塞通过滑轮和一重物连接并保持平衡，已知活塞距缸口0.2m，活塞面积10cm2，大气压强1.0×105Pa，物重50N，活塞质量及一切摩擦不计，缓慢升高环境温度，使活塞刚好升到缸口，封闭气体吸收了60J的热量，同时气体对外做功10J的功，则封闭气体的压强将
不变
不变
选填“增加”、“减小”或“不变”），气体内能变化量为
50
50
J．
（3）用油膜法测量分子大小的实验中，将浓度为的一滴油酸溶液，轻轻滴入水中，稳定后形成了一层单分子油膜，测得一滴油酸溶液的体积为V0，形成的油膜面积为S，则油酸分子的直径约为多少？如果把油酸分子看成是球形的，该滴油酸分子数约为多少？
B．（选修3-4模块）
（1）下列说法中正确的有
A．不管光源与观察者是否存在相对运动，观察者观察到的光速是不变的
B．水面上的油膜呈现彩色是光的干涉现象
C．在光导纤维束内传送图象是利用光的色散现象
D．声源向静止的观察者运动，观察者接收到的频率小于声源的频率
（2）如图1所示为一个向右传播的t=0时刻的横波波形图，已知波从O点传到D点用0.2s，该波的波速为
10
10
 m/s，频率为
2.5
2.5
 Hz；t=0时，图中“A、B、C、D、E、F、G、H、I、J”各质点中，向y轴正方向运动的速率最大的质点是
D
D

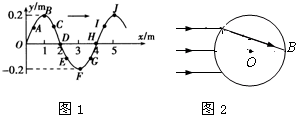（3）图2示是一透明的圆柱体的横截面，其半径R=20cm，折射率为
3
，AB是一条直径，今有一束平行光沿AB方向射向圆柱体，试求：
①光在圆柱体中的传播速度；
②距离直线AB多远的入射光线，折射后恰经过B点．
C．（选修模块3-5）
（1）下列说法正确的是
A．康普顿效应进一步证实了光的波动特性
B．为了解释黑体辐射规律，普朗克提出电磁辐射的能量的量子化
C．经典物理学不能解释原子的稳定性和原子光谱的分立特征
D．天然放射性元素的半衰期与环境的温度有关
（2）90234Th是不稳定的，能自发地发生衰变．
①完成90234Th衰变反应方程90234Th→91234Pa+．
②90234Th衰变为86222Rn，共经过
3
3
  次α衰变，
2
2
 次β衰变．
（3）光滑水平上有A、B两辆小车，A、B两车上分别固定一根条形磁铁和两根条形磁铁（条形磁铁是相同的），已知A车（包括车上的磁铁）的质量是B车（包括车上的磁铁）质量的4倍，当A车以已知速度v向静止的B车运动时，当它们之间的距离缩短到某一极限值后又被弹开，然后各自以新的速度做匀速直线运动，设作用前后它们的轨迹在同一直线上，求当A、B之间距离最短时它们各自的速度．

如图所示，用某种透明材料制成一块等腰直角棱镜ABC，光线从AB面入射，调整到入解角i，当i＝时，它射入棱镜后在AC面上折射时，其折射线恰好沿AC方向射出．试求该棱镜的折射率n．其中sin(α＋β)＝sinαcosβ＋cosαsinβ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网