题目内容
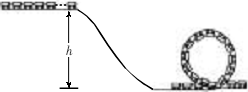
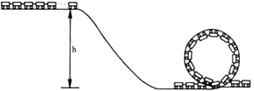
过山车质量均匀分布,从高为h的平台上无动力冲下倾斜轨道并进入水平轨道,然后进入竖直圆形轨道,如图17,已知过山车的质量为M,长为L,每节车厢长为a,竖直圆形轨道半径为R, L> 2πR,且R>>a,可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向,为了不出现脱轨的危险,h至少为多少?(用R、L表示,认为运动时各节车厢速度大小相等,且忽略一切摩擦力及空气阻力)
![]()
解析:
取过山车为研究对象,过山车从平台上滑下到车厢占满竖直圆形轨道过程中,由于只有重力做功,故机械能守恒,竖直圆形轨道上的过山车可以把这部分的重心看作在轨道的圆心上,所以有:
![]() ①(4 分)
①(4 分)
在竖直方向受到重力和轨道对它向下的压力,受力分析如图所示,设一节车厢质量为m,则有:
![]() ② (3 分)N≥0 ③ (3 分)
② (3 分)N≥0 ③ (3 分)
联立解得 ![]() (4分)
(4分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目