��Ŀ����
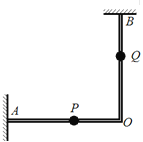
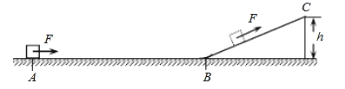
����Ŀ��С���������ϵ� A ���Գ��ٶ� 3 ��/������������ߵ� B ���׳����䵽�����ϵ� D �㡣��֪ AB ��� 0.5 ����������صĸ߶�Ϊ 1.25 ������� D �� B ��ˮƽ����Ϊ 1 �ף��������ٶ�ȡg=10m/s2
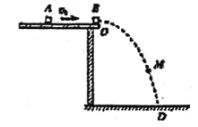
(1)�����������֮��Ļ���Ħ��������
(2)Ϊ���о�����ӹ⻬�����߹�����������»����˶���������һ����С���ƽ�����ȫ��ͬ�Ĺ⻬ ����������ù���̶����� OD �����غϵ�λ����������ظù�������»�(��������A �»������в��� ������)
a����С��鼴�����ʱ��ˮƽ���ٶ�
b������֤С����ع�����ٶ��»����Ͷ˵�ʱ����ڴ� B ��������������ʱ����
���𰸡���1��0.5��2��a.![]() ��b.֤�����̼�����.
��b.֤�����̼�����.
��������
��1�������ƽ���˶������㣺x=vBt�� h=![]() gt2
gt2
���vB=2m/s
��A��B�ɶ��ܶ�����![]()
��æ�=0.5
��2��a.�������ƽ���˶��������ʱ���ٶȷ�����ˮƽ����ļн�Ϊ��![]() ����
����![]() ��
��
�����������߹���»�������˵��ٶȴ�С���㣺![]() ��
��
���vD=5m/s
����鼴�����ʱ��ˮƽ���ٶ���![]()
b.���������������˶�ʱ����ֱ������ٶ�Ϊg���������߹���»�ʱ����ֱ����������������ϵĹ����֧�����ķ���������ֱ����ļ��ٶ�С��g������h=![]() at2��֪��С����ع�����ٶ��»����Ͷ˵�ʱ����ڴ� B ��������������ʱ�䡣
at2��֪��С����ع�����ٶ��»����Ͷ˵�ʱ����ڴ� B ��������������ʱ�䡣

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�