题目内容
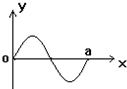
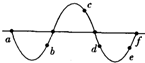
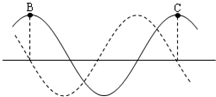
在一列沿水平直线传播的简谐横波上,其振幅为A.有相距0.4m的B、C两质点,t1=0时,B、C两质点的位移为正的最大值,而且B、C间有一个波谷.当t2=0.1s时,B、C两质点的位置刚好在各自的平衡位置,并且这时B、C间呈现一个波峰一个波谷,波谷到B点的距离为波长的四分之一,试求:
(1)该简谐横波的周期、波速各为多少?
(2)若波速为27m/s,则以t2时刻为计时起点,写出质点C的振动方程.
(1)该简谐横波的周期、波速各为多少?
(2)若波速为27m/s,则以t2时刻为计时起点,写出质点C的振动方程.
(1)首先可以判断,B、C相隔一个波长,根据因为在t1=0s时,B,C两个质点的位移为正的最大位移,而且B、C间有一个波谷.故波长λ=0.4m
如果波是从B向C传播的话,那么就是说在这段时间内波通过的位移是 x1=(n+
)λ,所以波速 v1=
=
=(4n+3)m/s,周期 T1=
=
s(n=0,1,2,3,…);
如果波是从C向B传播的话,在这段时间内的位移 x2=(n+
)λ,波速 v2=
=
=(4n+1)m/s,T2=
s,(n=0,1,2,3,…);
(2)当v=27m/s时,满足v=(4n+3)m/s,所以根据前面所求的,可知波的传播方向是B向C
位移x=vt=27×0.1=2.7m=6
λ,所以C点在平衡位置,且向上运动
则以t2时刻为计时起点,质点C的振动方程为 y=Asin
t=Asin
t=Asin5πt
答:
(1)该简谐横波从B向C传播时,周期、波速分别为:
s、(4n+3)m/s,(n=0,1,2,3,…);
从C向B传播时,周期、波速分别为:
s,(4n+1)m/s,(n=0,1,2,3,…).
(2)若波速为27m/s,则以t2时刻为计时起点,质点C的振动方程为y=Asin5πt.
如果波是从B向C传播的话,那么就是说在这段时间内波通过的位移是 x1=(n+
| 3 |
| 4 |
| x1 |
| t |
(n+
| ||
| 0.1 |
| λ |
| v1 |
| 0.4 |
| 4n+3 |
如果波是从C向B传播的话,在这段时间内的位移 x2=(n+
| 1 |
| 4 |
| x2 |
| t |
(n+
| ||
| t |
| 0.4 |
| 4n+1 |
(2)当v=27m/s时,满足v=(4n+3)m/s,所以根据前面所求的,可知波的传播方向是B向C
位移x=vt=27×0.1=2.7m=6
| 3 |
| 4 |
则以t2时刻为计时起点,质点C的振动方程为 y=Asin
| 2π |
| T |
| 2π |
| 0.4 |
答:
(1)该简谐横波从B向C传播时,周期、波速分别为:
| 0.4 |
| 4n+3 |
从C向B传播时,周期、波速分别为:
| 0.4 |
| 4n+1 |
(2)若波速为27m/s,则以t2时刻为计时起点,质点C的振动方程为y=Asin5πt.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目