题目内容
如图,一高为h=0.2m的木板B置于粗糙水平地面上,B的上表面以O点为界,O点右侧是光滑的,O点左侧是粗糙的。O点离木板B最右端的距离L=1.25m,O点离木板B最左端的距离S=0.32m。在B的最右端放一个质量与B相同的木块A,木块A可看成质点。A、B均处于静止状态,已知木板B与地面之间的动摩擦因数为μ1=0.1,A、B之间动摩擦因数为μ2=0.2,A、B的质量均为m。现给B一个水平向右的瞬间冲量,使B获得初速度v0=3.0m/s,求:
(1)当木板B向右运动1.25m时,A、B各自的速度大小;
(2)若木板B向右运动1.25m时,木板B突然受到一个向右的水平作用力F=0.2mg,则水平力F作用于木板B的时间为0.4s时,木块A离O点的水平距离。

(1)在O点右侧,木块A受到的摩擦力为零,故木块A静止不动,
即![]()
B在地面的摩擦力作用下做匀减速运动。设B向右运动1.25m时的速度为vB,
对B由动能定理,得
![]() ①
①
解①得![]()
(2)当木板B突然受力F后,木块A做加速运动、木板B做减速运动,设A、B最后达到的共同速度为v共,A、B发生相对运动到达共同速度阶段A在B上滑行的距离为S0
由动量守恒定律,得![]() ②
②
由能量守恒定律,得![]() ③
③
解②③得S0=0.5m
由于S0>S,则说明A将从B 上表面滑落.设A刚好滑离B时A、B的速度分别为vA、vB,
由动量守恒定律,得 ![]() ④
④
由能量守恒定律,得 ![]() ⑤
⑤
解④⑤得 ![]()
设A在B上自O点至离开B所用的时间为t1,
对A,由动量定理,有![]() ⑥
⑥
解⑥式得t1=0.2s
此后A以vA为初速度向右作平抛运动,设A经t2落地,t2时间内A的水平位移为x
由平抛运动规律有:
![]() ⑦
⑦
![]() ⑧
⑧
解⑦⑧得 ![]()
当A作平抛运动的同时,B向右作初速度为![]() 的匀加速运动。设其加速度为
的匀加速运动。设其加速度为![]()
由牛顿第二定律,有![]() ⑨
⑨
设t2内B运动的距离为SB
![]() ⑩
⑩
则B受F作用0.4s时A离O点的水平距离
![]()
![]()
解⑨⑩![]() 得△S=0.58m。
得△S=0.58m。

 为了测定一小金属滑块与木板之间的动摩擦因数,某人设计了如图所示的实验:将一长L=1m的木板在一高出地面的平台上搭成一高为H=0.6m的斜面,并在木板末端连接一小段光滑的圆弧轨道,使滑块从斜面上滑下到达末端时速度方向能平滑地过渡为水平方向,滑块离开轨道后飞行一段时间落到水平地面上.他让滑块从斜面上不同高度处由静止滑下,测出每次滑块在斜面上下滑的高度h,并测出相应的滑块离开轨道后落到水平面上时发生的水平位移s.不计空气阻力的影响.
为了测定一小金属滑块与木板之间的动摩擦因数,某人设计了如图所示的实验:将一长L=1m的木板在一高出地面的平台上搭成一高为H=0.6m的斜面,并在木板末端连接一小段光滑的圆弧轨道,使滑块从斜面上滑下到达末端时速度方向能平滑地过渡为水平方向,滑块离开轨道后飞行一段时间落到水平地面上.他让滑块从斜面上不同高度处由静止滑下,测出每次滑块在斜面上下滑的高度h,并测出相应的滑块离开轨道后落到水平面上时发生的水平位移s.不计空气阻力的影响. A.必须同时知道当地的重力加速度g和平台的高度Y
A.必须同时知道当地的重力加速度g和平台的高度Y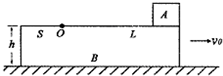 如图,一高为h=0.2m的木板B置于粗糙水平地面上,B的上表面以O点为界,O点右侧是光滑的,O点左侧是粗糙的.O点离木板B最右端的距离L=1.25m,O点离木板B最左端的距离S=0.32m.在B的最右端放一个质量与B相同的木块A,木块A可看成质点.A、B均处于静止状态,已知木板B与地面之间的动摩擦因数为μ1=0.1,A、B之间动摩擦因数为μ2=0.2,A、B的质量均为m.现给B一个水平向右的瞬间冲量,使B获得初速度v0=3.0m/s,求:
如图,一高为h=0.2m的木板B置于粗糙水平地面上,B的上表面以O点为界,O点右侧是光滑的,O点左侧是粗糙的.O点离木板B最右端的距离L=1.25m,O点离木板B最左端的距离S=0.32m.在B的最右端放一个质量与B相同的木块A,木块A可看成质点.A、B均处于静止状态,已知木板B与地面之间的动摩擦因数为μ1=0.1,A、B之间动摩擦因数为μ2=0.2,A、B的质量均为m.现给B一个水平向右的瞬间冲量,使B获得初速度v0=3.0m/s,求: 如图所示,一质量为M=0.4kg的滑块由光滑弧形凹槽和粗糙水平薄板平滑连接而成,薄板的长度为L=0.3m,厚度忽略不计.将该滑块固定在一高为H=0.8m的光滑水平桌面上,且薄板的右端点与桌子边缘平齐.将一质量为m=0.2kg的小物块(可视为质点)在弧形凹槽上某点由静止释放,小物块落地时距桌面边缘的水平距离为S=0.4m.已知小物块与薄板的动摩擦因数为μ=0.5,空气阻力忽略不计,g取10m/s2.
如图所示,一质量为M=0.4kg的滑块由光滑弧形凹槽和粗糙水平薄板平滑连接而成,薄板的长度为L=0.3m,厚度忽略不计.将该滑块固定在一高为H=0.8m的光滑水平桌面上,且薄板的右端点与桌子边缘平齐.将一质量为m=0.2kg的小物块(可视为质点)在弧形凹槽上某点由静止释放,小物块落地时距桌面边缘的水平距离为S=0.4m.已知小物块与薄板的动摩擦因数为μ=0.5,空气阻力忽略不计,g取10m/s2.
