题目内容
（2009?佛山三模）如图所示，与纸面垂直的竖直面MN的左侧空间中存在竖直向上场强大小为E的匀强电场（上、下及左侧无界）．一个质量为m、电量为q=mg/E的可视为质点的带正电小球，在t=0时刻以大小为V0的水平初速度向右通过电场中的一点P，当t=t1时刻在电场所在空间中加上一如图所示随时间周期性变化的磁场，使得小球能竖直向下通过D点，D为电场中小球初速度方向上的一点，PD间距为L，D到竖直面MN的距离DQ为L/π．设磁感应强度垂直纸面向里为正．
（1）如果磁感应强度B0为已知量，试推出满足条件时t1的表达式（用题中所给物理量的符号表示）
（2）若小球能始终在电场所在空间做周期性运动．则当小球运动的周期最大时，求出磁感应强度B0及运动的最大周期T的大小．
（3）当小球运动的周期最大时，在图中画出小球运动一个周期的轨迹．
（1）如果磁感应强度B0为已知量，试推出满足条件时t1的表达式（用题中所给物理量的符号表示）
（2）若小球能始终在电场所在空间做周期性运动．则当小球运动的周期最大时，求出磁感应强度B0及运动的最大周期T的大小．
（3）当小球运动的周期最大时，在图中画出小球运动一个周期的轨迹．
分析：（1）小球在磁场中做匀速圆周运动，根据洛伦兹力提供向心力，结合牛顿第二定律与几何关系，即可求解；
（2）根据小球做匀速圆周运动，由几何关系与运动轨道周期的公式，即可求解；
（3）根据对小球受力分析，由受力情况来确定运动情况，从而画出运动轨迹．
（2）根据小球做匀速圆周运动，由几何关系与运动轨道周期的公式，即可求解；
（3）根据对小球受力分析，由受力情况来确定运动情况，从而画出运动轨迹．
解答：解：当小球进入电场时：mg=Eq将做匀速直线运动
（1）在t1时刻加入磁场，小球在时间t0内将做匀速圆周运动，圆周运动周期为T0
若竖直向下通过D点，由图甲1分析可知必有以下两个条件：
t0=
T0
PF-PD=R 即：V0t1-L=R
qV0B0=
所以：V0t1-L=
t1=
+
（2）小球运动的速率始终不变，当R变大时，T0也增加，小球在电场中的运动的周期T增加，
在小球不飞出电场的情况下，当T最大时有：
DQ=2R
=2
B0=
T0=
=
=
由图分析可知小球在电场中运动的最大周期：
T=8×
T0=
（3）如图
答：（1）推出满足条件时t1的表达式t1=
+
；
（2）则出磁感应强度B0及运动的最大周期T的大小8×
T0=
．
（3）当小球运动的周期最大时，在图中画出小球运动一个周期的轨迹如上图所示．
（1）在t1时刻加入磁场，小球在时间t0内将做匀速圆周运动，圆周运动周期为T0
若竖直向下通过D点，由图甲1分析可知必有以下两个条件：
t0=
| 3 |
| 4 |
PF-PD=R 即：V0t1-L=R
qV0B0=
m
| ||
| R |
所以：V0t1-L=
| mv0 |
| qB0 |
t1=
| L |
| v0 |
| m |
| qB0 |
（2）小球运动的速率始终不变，当R变大时，T0也增加，小球在电场中的运动的周期T增加，
在小球不飞出电场的情况下，当T最大时有：
DQ=2R
| L |
| π |
| mv0 |
| qB0 |
B0=
| 2πmv0 |
| qL |
T0=
| 2πR |
| v0 |
| 2πm |
| qB0 |
| L |
| v0 |
由图分析可知小球在电场中运动的最大周期：
T=8×
| 3 |
| 4 |
| 6L |
| v0 |
（3）如图
答：（1）推出满足条件时t1的表达式t1=
| L |
| v0 |
| m |
| qB0 |
（2）则出磁感应强度B0及运动的最大周期T的大小8×
| 3 |
| 4 |
| 6L |
| v0 |
（3）当小球运动的周期最大时，在图中画出小球运动一个周期的轨迹如上图所示．
点评：考查粒子在电场力与重力的匀速直线运动，及在电场力、磁场力与重力共同作用下的匀速圆周运动，掌握受力平衡的条件，理解几何关系在题目中的应用．注意左手定则中运动的电荷的正负电性．
练习册系列答案
相关题目
（2009?佛山三模）新华社北京10月24日电，24日18时29分，星箭成功分离之后，嫦娥一号卫星进入半径为205公里的圆轨道上绕地球做圆周运动，卫星在这个轨道上“奔跑”一圈半后，于25日下午进行第一次变轨，变轨后，卫星轨道半径将抬高到离地球约600公里的地方．已知地球半径为R，表面重力加速度为g，质量为m的嫦娥一号卫星在地球上空的万有引力势能为Ep=
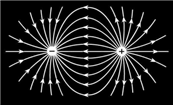（2009?佛山三模）如图是等量异种电荷形成电场的电场线，则以下说法正确的是（ ）
（2009?佛山三模）如图所示，固定的竖直光滑金属导轨间距为L，上端接有阻值为R的电阻，处在方向水平、垂直导轨平面向里的磁感应强度为B的匀强磁场中，质量为m的导体棒与下端固定的竖直轻质弹簧相连且始终保持与导轨接触良好，导轨与导体棒的电阻均可忽略，弹簧的劲度系数为k．初始时刻，弹簧恰好处于自然长度，使导体棒以初动能Ek沿导轨竖直向下运动，且导体棒在往复运动过程中，始终与导轨垂直．