题目内容
 (2009?佛山三模)新华社北京10月24日电,24日18时29分,星箭成功分离之后,嫦娥一号卫星进入半径为205公里的圆轨道上绕地球做圆周运动,卫星在这个轨道上“奔跑”一圈半后,于25日下午进行第一次变轨,变轨后,卫星轨道半径将抬高到离地球约600公里的地方.已知地球半径为R,表面重力加速度为g,质量为m的嫦娥一号卫星在地球上空的万有引力势能为Ep=
(2009?佛山三模)新华社北京10月24日电,24日18时29分,星箭成功分离之后,嫦娥一号卫星进入半径为205公里的圆轨道上绕地球做圆周运动,卫星在这个轨道上“奔跑”一圈半后,于25日下午进行第一次变轨,变轨后,卫星轨道半径将抬高到离地球约600公里的地方.已知地球半径为R,表面重力加速度为g,质量为m的嫦娥一号卫星在地球上空的万有引力势能为Ep=| mgR2 | r |
(1)质量为m的嫦娥一号卫星以速率v在某一圆轨道上绕地球做圆周运动,求此时卫星距地球地面高度h1;
(2)要使嫦娥一号卫星上升,从离地高度h1再增加h的轨道上做匀速圆周运动,卫星发动机至少要做多少功?
分析:1、卫星绕地球做圆周运动靠万有引力提供向心力,根据牛顿第二定律,结合万有引力等于重力求出轨道半径的大小,从而求出卫星距离地面的高度.
2、根据分别求出在离地高度h1和h1+h的轨道上的总机械能E1、E2,根据功能关系W=E2-E1,可计算卫星发动机至少要做的功.
2、根据分别求出在离地高度h1和h1+h的轨道上的总机械能E1、E2,根据功能关系W=E2-E1,可计算卫星发动机至少要做的功.
解答:解:(1)设地球质量为M,万有引力恒量为G,卫星距地面高度为h1时速度为v,
对卫星有G
=m
,对地面上物体有mg=G
,
解以上两式得h1=
-R.
(2)卫星在距地面高度h1的轨道做匀速圆周运动有G
=m
,得v2=
∴此时卫星的动能Ek1=
mv2=
=
,万有引力势能Ep1=-
,
卫星在距地面高度h1时的总机械能E1=Ek1+Ep1=
-
=-
.
同理,卫星在距地面高度(h1+h)时的总机械能E2=-
.
由功能关系,卫星发动机至少要做功 W=E2-E1=
.
答:(1)质量为m的嫦娥一号卫星以速率v在某一圆轨道上绕地球做圆周运动,则此时卫星距地球地面高度h1为
-R.
(2)要使嫦娥一号卫星上升,从离地高度h1再增加h的轨道上做匀速圆周运动,则卫星发动机至少要做功为
.
对卫星有G
| Mm |
| (R+h1)2 |
| v2 |
| R+h1 |
| Mm |
| R2 |
解以上两式得h1=
| gR2 |
| v2 |
(2)卫星在距地面高度h1的轨道做匀速圆周运动有G
| Mm |
| (R+h1)2 |
| v2 |
| R+h1 |
| GM |
| (R+h1) |
∴此时卫星的动能Ek1=
| 1 |
| 2 |
| GMm |
| 2(R+h1) |
| mgR2 |
| 2(R+h1) |
| mgR2 |
| R+h1 |
卫星在距地面高度h1时的总机械能E1=Ek1+Ep1=
| mgR2 |
| 2(R+h1) |
| mgR2 |
| R+h1 |
| mgR2 |
| 2(R+h1) |
同理,卫星在距地面高度(h1+h)时的总机械能E2=-
| mgR2 |
| 2(R+h1+h) |
由功能关系,卫星发动机至少要做功 W=E2-E1=
| mgR2h |
| 2(R+h1)(R+h1+h) |
答:(1)质量为m的嫦娥一号卫星以速率v在某一圆轨道上绕地球做圆周运动,则此时卫星距地球地面高度h1为
| gR2 |
| v2 |
(2)要使嫦娥一号卫星上升,从离地高度h1再增加h的轨道上做匀速圆周运动,则卫星发动机至少要做功为
| mgR2h |
| 2(R+h1)(R+h1+h) |
点评:解决本题的关键掌握万有引力提供向心力G
=m
以及万有引力等于重力这两大理论.
| Mm |
| r2 |
| v2 |
| r |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

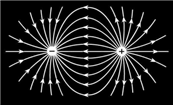 (2009?佛山三模)如图是等量异种电荷形成电场的电场线,则以下说法正确的是( )
(2009?佛山三模)如图是等量异种电荷形成电场的电场线,则以下说法正确的是( ) (2009?佛山三模)如图所示,固定的竖直光滑金属导轨间距为L,上端接有阻值为R的电阻,处在方向水平、垂直导轨平面向里的磁感应强度为B的匀强磁场中,质量为m的导体棒与下端固定的竖直轻质弹簧相连且始终保持与导轨接触良好,导轨与导体棒的电阻均可忽略,弹簧的劲度系数为k.初始时刻,弹簧恰好处于自然长度,使导体棒以初动能Ek沿导轨竖直向下运动,且导体棒在往复运动过程中,始终与导轨垂直.
(2009?佛山三模)如图所示,固定的竖直光滑金属导轨间距为L,上端接有阻值为R的电阻,处在方向水平、垂直导轨平面向里的磁感应强度为B的匀强磁场中,质量为m的导体棒与下端固定的竖直轻质弹簧相连且始终保持与导轨接触良好,导轨与导体棒的电阻均可忽略,弹簧的劲度系数为k.初始时刻,弹簧恰好处于自然长度,使导体棒以初动能Ek沿导轨竖直向下运动,且导体棒在往复运动过程中,始终与导轨垂直.