题目内容
11.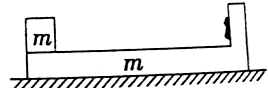 在光滑水平面上有一带挡板的长木板,其质量为m,长度为L(挡板的厚度可忽略),木板左端有一质量也是m(可视为质点)的滑块,挡板上固定有一个小炸药包,如图所示(小炸药包长度以及质量与长木板相比可忽略),滑块与木板间的动摩擦因数恒定,整个系统处于静止状态.给滑块一个水平向右的初速度v0,滑块相对木板向右运动,刚好能与炸药包接触,此时小炸药包爆炸(此过程时间极短,爆炸后滑块和木板只在水平方向运动,且完好无损),滑块最终又回到木板的左端,恰与木板相对静止,求:
在光滑水平面上有一带挡板的长木板,其质量为m,长度为L(挡板的厚度可忽略),木板左端有一质量也是m(可视为质点)的滑块,挡板上固定有一个小炸药包,如图所示(小炸药包长度以及质量与长木板相比可忽略),滑块与木板间的动摩擦因数恒定,整个系统处于静止状态.给滑块一个水平向右的初速度v0,滑块相对木板向右运动,刚好能与炸药包接触,此时小炸药包爆炸(此过程时间极短,爆炸后滑块和木板只在水平方向运动,且完好无损),滑块最终又回到木板的左端,恰与木板相对静止,求:(1)滑块刚好能与小炸药包接触时滑块的速度;
(2)小炸药包爆炸完时,滑块和木板的速度.
分析 (1)滑块相对木板向右运动,刚好能与炸药包接触,说明此时滑块和长木板的速度相同,根据动量守恒定律列式求解;
(2)设爆炸后滑块和木板的速度分别为v1′,v2′,最终滑块相对静止于木板的左端时速度为v2,系统在爆炸过程、爆炸前后动量守恒,能量守恒,根据动量守恒定律及能量守恒定律列式即可求解.
解答 解:(1)滑块相对木板向右运动,刚好能与炸药包接触,说明此时滑块和长木板的速度相同,设滑块刚要与炸药包接触时的速度为v1,
滑块和木板系统在爆炸前动量守恒,根据动量守恒定律得:mv0=2mv1①
解得:v1=$\frac{{v}_{0}}{2}$,方向水平向右,
(2)对滑块与木板系统在爆炸前应用功能关系:
μmgL=$\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}×2m×{{v}_{1}}^{2}$②
设爆炸后滑块和木板的速度分别为v1′,v2′,最终滑块相对静止于木板的左端时速度为v2,
系统在爆炸过程、爆炸前后动量守恒:
mv0=mv1′+mv2′③
mv0=2mv2④
对系统在爆炸后应用功能关系:
μmgL=$\frac{1}{2}m{{v}_{1}′}^{2}+\frac{1}{2}m{{v}_{2}′}^{2}-\frac{1}{2}×2m{{v}_{2}}^{2}$⑤
由②③④⑤解得v1′=0;v2′=v0,方向水平向右.
答:(1)滑块刚好能与小炸药包接触时滑块的速度大小为$\frac{{v}_{0}}{2}$,方向水平向右;
(2)小炸药包爆炸完时,滑块的速度大为0,木板的速度大小为v0,方向水平向右.
点评 本题的关键是分析清楚物体运动过程、应用动量守恒定律与能量守恒定律解题,抓住临界条件,知道滑块相对木板向右运动,刚好能与炸药包接触,说明此时滑块和长木板的速度相同,难度适中.

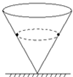 一圆锥开口向上竖直放置,让一小钢球沿光滑内壁做水平方向的匀速圆周运动,如图所示.由于空气阻力的作用,小钢球运动的圆平面会很缓慢地降低,则下列关于小钢球的变化情况正确的是( )
一圆锥开口向上竖直放置,让一小钢球沿光滑内壁做水平方向的匀速圆周运动,如图所示.由于空气阻力的作用,小钢球运动的圆平面会很缓慢地降低,则下列关于小钢球的变化情况正确的是( )| A. | ω逐渐增大,向心加速度大小不变 | B. | ω逐渐减小,a逐渐增大 | ||
| C. | 向心力减小,线速度增大 | D. | 向心力大小不变,线速度减小 |
 如图所示,P、Q为带等量负电荷的点电荷,O为其连线的中点,A、B为其中垂线上的两点,则下列说法中正确的是( )
如图所示,P、Q为带等量负电荷的点电荷,O为其连线的中点,A、B为其中垂线上的两点,则下列说法中正确的是( )| A. | 负电荷在A点的电势能大于在B点的电势能 | |
| B. | 正电荷在A点的电势能大于在B点的电势能 | |
| C. | A点的场强一定大于B点的场强 | |
| D. | 将带正电的试探电荷从A移动到B点过程中,电场力做正功 |
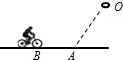 学校组织“骑车投球”比赛,甲、乙两参赛者沿规定直轨道匀速骑行过程中,将手中网球沿垂直于骑行方向水平抛向地面上的塑料筐O中,如图,A点是轨道上离框最近的点.甲以3m/s的速度骑行,在B点将网球以速度v水平抛出,网球恰好落入筐中;乙以4m/s的速度骑行,要想将球投入筐中,乙参赛者应(不计空气阻力),( )
学校组织“骑车投球”比赛,甲、乙两参赛者沿规定直轨道匀速骑行过程中,将手中网球沿垂直于骑行方向水平抛向地面上的塑料筐O中,如图,A点是轨道上离框最近的点.甲以3m/s的速度骑行,在B点将网球以速度v水平抛出,网球恰好落入筐中;乙以4m/s的速度骑行,要想将球投入筐中,乙参赛者应(不计空气阻力),( )| A. | 在到达B点之后将球抛出 | B. | 在到达B点之前将球抛出 | ||
| C. | 将球也以速度v水平抛出 | D. | 将球以大于v的速度水平抛出 |
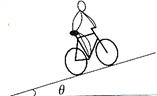 如图所示为小明下课回家骑车上坡的情形,假如他骑车时的最大功率恒为P=1200W,车和人的总质量为75kg,斜坡倾角为20°,运动过程中所受到的摩擦阻力恒为Ff=60N,取g=10m/s2,sin20°=0.34,则:
如图所示为小明下课回家骑车上坡的情形,假如他骑车时的最大功率恒为P=1200W,车和人的总质量为75kg,斜坡倾角为20°,运动过程中所受到的摩擦阻力恒为Ff=60N,取g=10m/s2,sin20°=0.34,则: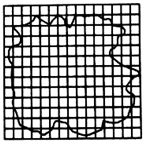 在“用油膜法估测分子大小”实验中,油酸酒精溶液浓度为每104mL溶液中有纯油酸7mL.用注射器测得1mL上述溶液为70滴.把一滴该溶液滴人盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用彩笔在玻璃板上描出油酸的轮廊,再把玻璃板放在坐标纸上,其形状和尺寸如图所示.坐标中正方形方格的边长为1cm,试求:
在“用油膜法估测分子大小”实验中,油酸酒精溶液浓度为每104mL溶液中有纯油酸7mL.用注射器测得1mL上述溶液为70滴.把一滴该溶液滴人盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用彩笔在玻璃板上描出油酸的轮廊,再把玻璃板放在坐标纸上,其形状和尺寸如图所示.坐标中正方形方格的边长为1cm,试求: