题目内容
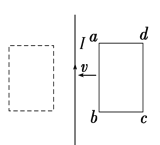
【题目】在平面直角坐标系x0y中,第I象限内存在垂直于坐标平面向里的匀强磁场,在A(L,0)点有一粒子源,沿y轴正向发射出速率分别为υ、5υ、9υ的同种带电粒子,粒子质量为m,电荷量为q。在B(0,L)、C(0,3L)、D(0,5L)放一个粒子接收器,B点的接收器只能吸收来自y轴右侧到达该点的粒子,C、D两点的接收器可以吸收沿任意方向到达该点的粒子。已知速率为υ的粒子恰好到达B点并被吸收,不计粒子重力。
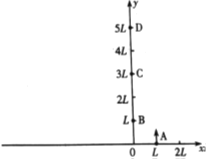
(1)求第I象限内磁场的磁感应强度B1;
(2)计算说明速率为5v、9v的粒子能否到达接收器;
(3)若在第Ⅱ象限内加上垂直于坐标平面的匀强磁场,使所有粒子均到达接收器,求所加磁场的磁感应强度B2的大小和方向。
【答案】(1)![]() (2)故速率为
(2)故速率为![]() 的粒子被吸收,速率为
的粒子被吸收,速率为![]() 的粒子不能被吸收(3)
的粒子不能被吸收(3)![]() (或
(或![]() ),垂直坐标平面向外
),垂直坐标平面向外
【解析】
(1)由几何关系知,速率为![]() 的粒子在第Ⅰ象限内运动的半径为
的粒子在第Ⅰ象限内运动的半径为![]() ①
①
由牛顿运动定律得![]() ②
②
得![]() ③
③
(2)由(1)中关系式可得速率为![]() 、
、![]() 的粒子在磁场中的半径分别为
的粒子在磁场中的半径分别为![]() 、
、![]() .
.
设粒子与![]() 轴的交点到
轴的交点到![]() 的距离为
的距离为![]() ,将
,将![]() 和
和![]() 分别代入下式
分别代入下式
![]() ④
④
得这两种粒子在![]() 轴上的交点到
轴上的交点到![]() 的距离分别为
的距离分别为![]() 、
、![]() ⑤
⑤
故速率为![]() 的粒子被吸收,速率为
的粒子被吸收,速率为![]() 的粒子不能被吸收。⑥
的粒子不能被吸收。⑥
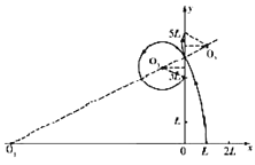
(3)若速度为![]() 的粒子能到达
的粒子能到达![]() 点的接收器,则所加磁场应垂直坐标平面向外⑦
点的接收器,则所加磁场应垂直坐标平面向外⑦
设离子在所加磁场中的运动半径为![]() ,由几何关系有
,由几何关系有
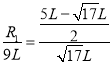 ⑧
⑧
又![]() ⑨
⑨
解得![]() (或
(或![]() )⑩
)⑩
若粒子到达![]() 点的接收器,所加磁场应垂直于坐标平面向里
点的接收器,所加磁场应垂直于坐标平面向里
同理: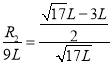
![]()
解得![]() (或
(或![]() )
)

练习册系列答案
相关题目