题目内容
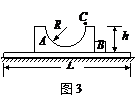 如图3所示,长为L的光滑平台固定在地面上,平台中间放有小物体A和B,两者彼此接触。A的上表面是半径为R的半圆形轨道,轨道顶端距台面的高度为h处,有一个小物体C,A、B、C的质量均为m。在系统静止时释放C,已知在运动过程中,A、C始终接触,试求:
如图3所示,长为L的光滑平台固定在地面上,平台中间放有小物体A和B,两者彼此接触。A的上表面是半径为R的半圆形轨道,轨道顶端距台面的高度为h处,有一个小物体C,A、B、C的质量均为m。在系统静止时释放C,已知在运动过程中,A、C始终接触,试求:
⑴ 物体A和B刚分离时,B的速度;
⑵ 物体A和B分离后,C所能达到的距台面的最大高度;
⑶ 试判断A从平台的哪边落地,并估算A从与B分离到落地所经历的时间。
⑴VB=![]()
⑵l=h-![]()
⑶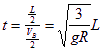
解析:
⑴ 当C运动到半圆形轨道的最低点时,A、B将开始分开。在此以前的过程中,由A、B、C三个物体组成的系统水平方向的动量守恒和机械能守恒,可得:
mVA+mVB +mVC=0
mgR=![]() mVA2+
mVA2+![]() mVB2+
mVB2+![]() mVC2
mVC2
而VA=VB
可解得:VB=![]()
⑵ A、B分开后,A、C两物体水平方向的动量和机械能都守恒。C到最高点时,A、C速度都是V,C能到达的距台面的最大高度为l,则
mVB=2mV
mg(l+R-h)+![]() (2m)V2=
(2m)V2=![]() mVA2+
mVA2+![]() mVC2
mVC2
可解得:l=h-![]()
⑶ 很明显,A、C从平台左边落地。
因为L>>R,所以可将A、C看成一个质点,速度为![]() VB,落下平台的时间
VB,落下平台的时间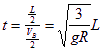

练习册系列答案
相关题目
 如图甲所示,相距为L的光滑足够长平行金属导轨水平放置,导轨一部分处在垂直于导轨平面的匀强磁场中,OO′为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距OO′为L处垂直导轨放置一质量为m、电阻不计的金属杆ab.若ab杆在恒力作用下由静止开始向右运动,其速度v-位移x的关系图象如图乙所示,则
如图甲所示,相距为L的光滑足够长平行金属导轨水平放置,导轨一部分处在垂直于导轨平面的匀强磁场中,OO′为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距OO′为L处垂直导轨放置一质量为m、电阻不计的金属杆ab.若ab杆在恒力作用下由静止开始向右运动,其速度v-位移x的关系图象如图乙所示,则