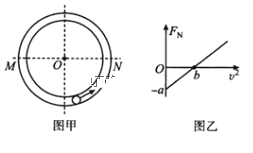
��Ŀ����
����Ŀ����ͼ��ʾ��һ�����=37����б�����һ���ʹ����������B�㣬���ʹ���v=6m/s���ٶ�˳ʱ��ת������һС����б�涥�˵�����0=4m/s�ij��ٶ���б���»�������黬��б��ĵ˵�ʱ�ٶ�ǡ��Ϊ�㣬Ȼ���ڴ��ʹ��Ĵ����£��Ӵ��ʹ��Ҷ˵�C��ˮƽ�׳�������䵽�����ϵ�D�㣬��֪б�泤��L1=8m�����ʹ�����L2=18m������봫�ʹ�֮��Ķ�Ħ��������2=0.3����sin37��=0.6��cos37��=0.8��g=10m/s2����
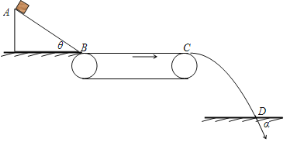
��1���������б��֮��Ķ�Ħ��������l��
��2��������ڴ��ʹ����˶�ʱ�䣻
��3���������D����ٶȷ��������н�Ϊa=53������C�㵽����ĸ߶Ⱥ�C��D������ˮƽ���롣
���𰸡���1��![]()
��2��4s��
��3��4.8m��
��������
���⣨1����A��B�ɶ��ܶ����������Ħ������
��2����ţ�ٵڶ���������ڴ��ʹ��ϵļ��ٶȣ��жϳ��ڴ��ʹ��ϵ��˶����̣����˶�ѧ��ʽ�������ʱ�䣻
��3��������ƽ���˶�������ֱ�������������˶���
�⣺��1����A��B�ɶ��ܶ�����֪
![]()
�������ݽ��![]()
��2������ڴ��ʹ�����ţ�ٵڶ����ɣ���2mg=ma
a=![]()
�ﵽ���ʹ��ٶ�����ʱ��Ϊt=![]() s
s
����ǰ��λ��Ϊ![]() ��18m
��18m
�����ڴ��ʹ����������˶�
�����˶�ʱ��Ϊ![]()
�ʾ�����ʱ��Ϊt��=t+t��=4s
��3����߶�Ϊh������ֱ�������ٶ�Ϊ![]()
![]()
�������h=3.2m
��������ʱ��Ϊ![]()
ˮƽλ��ΪxCD=vt��=6��0.8s=4.8m
�𣺣�1���������б��֮��Ķ�Ħ��������lΪ![]()
��2��������ڴ��ʹ����˶�ʱ��Ϊ4s��
��3���������D����ٶȷ��������н�Ϊa=53����C�㵽����ĸ߶�Ϊ3.2m��C��D������ˮƽ����Ϊ4.8m��