题目内容
【题目】如图所示，S处有一电子源，可向纸面内任意方向发射电子，平板MN垂直于纸面，在纸面内的长度L=9.1cm，中点O与S间的距离d＝4.55cm，MN与SO直线的夹角为θ，板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场，磁感应强度B＝2.0×10－4T，电子质量m＝9.1×10－31kg，电荷量e＝－1.6×10－19C，不计电子重力。电子源发射速度v＝1.6×106m/s的一个电子，该电子打在板上可能位置的区域的长度为l，则
A. θ＝90°时，l＝9.1cm B. θ＝60°时，l＝9.1cm
C. θ＝45°时，l＝4.55cm D. θ＝30°时，l＝4.55cm
【答案】AD
【解析】
电子在磁场中受洛伦兹力作用做匀速圆周运动，根据洛伦兹力大小计算公式和向心力公式有：evB＝
，解得电子圆周运动的轨道半径为：r＝
＝
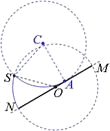
m＝4.55×10－2m＝4.55cm，恰好有：r＝d＝L/2，由于电子源S，可向纸面内任意方向发射电子，因此电子的运动轨迹将是过S点的一系列半径为r的等大圆，能够打到板MN上的区域范围如下图所示，实线SN表示电子刚好经过板N端时的轨迹，实线SA表示电子轨迹刚好与板相切于A点时的轨迹，因此电子打在板上可能位置的区域的长度为：l＝NA，
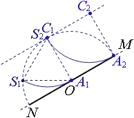
又由题设选项可知，MN与SO直线的夹角θ不定，但要使电子轨迹与MN板相切，根据图中几何关系可知，此时电子的轨迹圆心C一定落在与MN距离为r的平行线上，如下图所示，当l＝4.55cm时，即A点与板O点重合，作出电子轨迹如下图中实线S1A1，由图中几何关系可知，此时S1O与MN的夹角θ＝30°，故选项C错误；选项D正确；当l＝9.1cm时，即A点与板M端重合，作出电子轨迹如下图中实线S2A2，由图中几何关系可知，此时S2O与MN的夹角θ＝90°，故选项A正确；选项B错误。
