题目内容
7. 如图所示,在摩擦因数为μ的平面上竖直固定一半径为R的光滑半圆槽轨道,其底端恰与水平面相切,质量为m的小球以一定初速度从A点开始向右运动,经半圆槽轨道最低点B滚上半圆槽,小球恰能通过最高点C后落回到水平面上的A点. (不计空气阻力,已知m=1kg μ=0.25 R=$\frac{10}{6}$m 重力加速度g=10m/s2)求:
如图所示,在摩擦因数为μ的平面上竖直固定一半径为R的光滑半圆槽轨道,其底端恰与水平面相切,质量为m的小球以一定初速度从A点开始向右运动,经半圆槽轨道最低点B滚上半圆槽,小球恰能通过最高点C后落回到水平面上的A点. (不计空气阻力,已知m=1kg μ=0.25 R=$\frac{10}{6}$m 重力加速度g=10m/s2)求:(1)小球通过B点时对半圆槽的压力大小;
(2)小球的初速度v0.
分析 (1)对小球在B点时受力分析,根据牛顿第二定律求B受到的支持力,进而由牛顿第三定律得到B对圆槽的压力;
(2)小球恰能通过最高点C,即重力提供向心力,根据牛顿第二定律求出小球在C点的速度,小球离开C点后作平抛运动,根据平抛运动的特点求出AB两点间的距离.根据动能定理即可求出A点的初速度.
解答 解:(1)则mg=m$\frac{{v}_{C}^{2}}{R}$,vC=$\sqrt{gR}$
在B点小球做圆周运动,
F-mg=m$\frac{{v}_{B}^{2}}{R}$
得:F=mg+m$\frac{{v}_{B}^{2}}{R}$
B到C的过程中机械能守恒,得:$\frac{1}{2}m{v}_{C}^{2}+2mgR=\frac{1}{2}m{v}_{B}^{2}$
联立得:${v}_{B}=\sqrt{5gR}$,F=60N
由牛顿第三定律知小球通过B点时对半圆槽的压力大是60N;
(2)在C点小球恰能通过,故只有重力提供向心力,
过C点小球做平抛运动:sAB=vCt
h=$\frac{1}{2}$gt2
h=2R
联立以上各式可得sAB=2R.
由A到B的过程中摩擦力做功,得:$μmgs=\frac{1}{2}m{v}_{0}^{2}-\frac{1}{2}m{v}_{B}^{2}$
联立上几式可得:v0=10m/s
答:(1)小球通过B点时对半圆槽的压力大小是60N;
(2)小球的初速度是10m/s.
点评 本题关键是明确小球的运动情况,然后分过程运用平抛运动的分位移公式和向心力公式列式求解.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
18.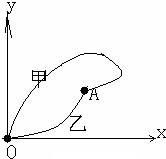 甲、乙两小分队进行代号为“猎狐”的军事演习,指挥部通过现代通讯设备,在屏幕上观察到两小分队的行军路线如图所示.两小分队同时从同一处O出发,最后同时捕“狐”于A点,则( )
甲、乙两小分队进行代号为“猎狐”的军事演习,指挥部通过现代通讯设备,在屏幕上观察到两小分队的行军路线如图所示.两小分队同时从同一处O出发,最后同时捕“狐”于A点,则( )
 甲、乙两小分队进行代号为“猎狐”的军事演习,指挥部通过现代通讯设备,在屏幕上观察到两小分队的行军路线如图所示.两小分队同时从同一处O出发,最后同时捕“狐”于A点,则( )
甲、乙两小分队进行代号为“猎狐”的军事演习,指挥部通过现代通讯设备,在屏幕上观察到两小分队的行军路线如图所示.两小分队同时从同一处O出发,最后同时捕“狐”于A点,则( )| A. | 两队行军路程x甲>x乙 | B. | 两队行军位移x甲>x乙 | ||
| C. | 两队平均速度v甲=v乙 | D. | 两队平均速度v甲>v乙 |
15.关于磁感线的说法中正确的是( )
| A. | 磁感线都不是封闭曲线 | |
| B. | 磁感线都是封闭曲线 | |
| C. | 电流磁场的磁感线是封闭曲线,磁体的磁感线不是封闭曲线 | |
| D. | 电流磁场的磁感线不是封闭曲线,磁体的磁感线是封闭曲线 |
2.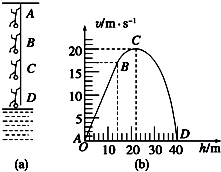 一质量为50kg的男孩在距离河流40m高的桥上做“蹦极跳”,原长长度为14m的弹性绳AB一端系着他的双脚,另一端则固定在桥上的A点,如图(a) 所示,然后男孩从桥面下坠直至贴近水面的最低点D.男孩的速率v跟下坠的距离h的变化关系如图(b)所示,假定绳在整个运动过程中遵守胡克定律(不考虑空气阻力、男孩的大小和绳的质量,g取10m/s2).下列说法正确的是( )
一质量为50kg的男孩在距离河流40m高的桥上做“蹦极跳”,原长长度为14m的弹性绳AB一端系着他的双脚,另一端则固定在桥上的A点,如图(a) 所示,然后男孩从桥面下坠直至贴近水面的最低点D.男孩的速率v跟下坠的距离h的变化关系如图(b)所示,假定绳在整个运动过程中遵守胡克定律(不考虑空气阻力、男孩的大小和绳的质量,g取10m/s2).下列说法正确的是( )
 一质量为50kg的男孩在距离河流40m高的桥上做“蹦极跳”,原长长度为14m的弹性绳AB一端系着他的双脚,另一端则固定在桥上的A点,如图(a) 所示,然后男孩从桥面下坠直至贴近水面的最低点D.男孩的速率v跟下坠的距离h的变化关系如图(b)所示,假定绳在整个运动过程中遵守胡克定律(不考虑空气阻力、男孩的大小和绳的质量,g取10m/s2).下列说法正确的是( )
一质量为50kg的男孩在距离河流40m高的桥上做“蹦极跳”,原长长度为14m的弹性绳AB一端系着他的双脚,另一端则固定在桥上的A点,如图(a) 所示,然后男孩从桥面下坠直至贴近水面的最低点D.男孩的速率v跟下坠的距离h的变化关系如图(b)所示,假定绳在整个运动过程中遵守胡克定律(不考虑空气阻力、男孩的大小和绳的质量,g取10m/s2).下列说法正确的是( )| A. | 男孩先做匀加速运动,后做变减速运动,最大位移为40m | |
| B. | 男孩的最大加速度会大于g | |
| C. | 系统储存的最大弹性势能为2×104 J | |
| D. | 弹性绳子的劲度系数为62.5N/m |
12.下列说法正确的是( )
| A. | 曲线运动可以是匀速运动,但是它一定是变速运动 | |
| B. | 平抛物体的加速度一定竖直向下,圆周运动的加速度一定指向圆心 | |
| C. | 做匀速圆周运动的物体,在任何相等的时间内通过的位移都相同 | |
| D. | 圆周运动的向心加速度方向始终与速度方向垂直 |
19. 一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )
一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )
 一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )
一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )| A. | 由A到C的过程中,物块的机械能守恒 | |
| B. | 由A到B的过程中,物块的动能和重力势能之和变大 | |
| C. | 由B到C的过程中,弹性势能的变化量与克服弹力做的功相等 | |
| D. | 由A到C的过程中,重力势能的减少量等于弹性势能的增加量 |
16. 如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )
如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )
 如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )
如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )| A. | 1~2s内质点的加速度大小为8m/s2 | B. | 2~4s内质点的位移大小为8m | ||
| C. | 3s末质点的速度为8m/s | D. | 3s末质点的加速度等于零 |
17. 如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )
如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )
 如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )
如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )| A. | $\frac{kQ}{{l}^{2}}$-$\frac{kQ}{{R}^{2}}$ | B. | $\frac{kQ}{{l}^{2}}$+$\frac{kQ}{{R}^{2}}$ | C. | 0 | D. | $\frac{kQ}{(l+R)^{2}}$ |
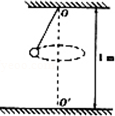 如图所示,质量是1kg的小球用长为0.5m的细线悬挂在O点,O点距地面高度为1m,如果使小球绕00′轴在水平面内做圆周运动,若细线最大承受拉力为12.5N,(g=10m/s2).求:
如图所示,质量是1kg的小球用长为0.5m的细线悬挂在O点,O点距地面高度为1m,如果使小球绕00′轴在水平面内做圆周运动,若细线最大承受拉力为12.5N,(g=10m/s2).求: