题目内容
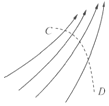
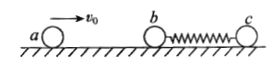
【题目】如图所示，竖直平面内有一段不光滑的斜直轨道与光滑的圆形轨道相切，切点P与圆心O的连线与竖直方向的夹角为θ=53°，圆形轨道的半径为R，一个质量为m的小物块从斜轨道上A点由静止开始下滑，然后沿圆形轨道运动，A点相对圆形轨道底部的高度h=7R，物块通过圆形轨道最高点C时，与轨道间的压力大小为3mg(sin53°=0.8，cos53°=0.6)。求：
(1)物块通过轨道最高点时的速度大小；
(2)物块通过轨道最低点B受轨道的支持力大小；
(3)物块与斜直轨道间的动摩擦因数μ。
【答案】(1)
；(2)
；(3)
【解析】
(1)对物块通过轨道最高点C时根据牛顿第二定律有
解得
(2)从最低点B到最高点C，根据机械能守恒有
物块通过轨道最低点B时，根据牛顿第二定律
联立解得
(3)设斜直轨道长为S，由A运动到B根椐动能定理有
解得
阅读快车系列答案
【题目】某次“探究加速度a跟物体所受合力F和质量m的关系”实验如下．
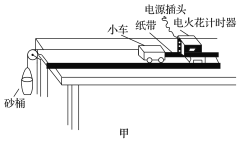
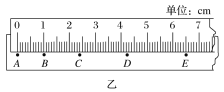
(1)图甲所示为实验装置图．图乙为某次实验得到的一段纸带，计数点A、B、C、D、E间的时间间隔为0.1 s，根据纸带可求出小车的加速度大小为________m/s2(结果保留两位有效数字)．
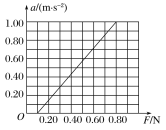
(2)保持小车质量不变，改变砂和砂桶质量，进行多次测量．根据实验数据作出了加速度a随拉力F的变化图线，如图所示．图中直线没有通过原点，其主要原因是_________.
(3)保持砂和砂桶质量不变，改变小车中砝码质量，进行多次测量，得到小车加速度a、质量m及其对应的
的数据如表中所示：
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
小车加速度a/(m·s－2) | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
小车和砝码质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
1/m/kg－1 | 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
a.请在图所示坐标纸中画出a－图线____________；
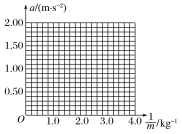
b．根据作出的a－图象可以得到的结论是：__________________________________.
