题目内容
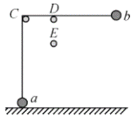
【题目】如图所示,a、b两个小球用一根不可伸长的细线连接,细线绕过固定光滑水平细杆C、与光滑水平细杆D接触,C、D在同一水平线上,D到小球6的距离为L,在D的正下方也固定有一光滑水平细杆E,D、E间的距离为![]() .小球a放在水平地面上,细线水平拉直,由静止释放小球b.当细线与水平细杆E接触的一瞬间,小球a对地面的压力恰好为零,不计小球的大小,则下列说法正确的是
.小球a放在水平地面上,细线水平拉直,由静止释放小球b.当细线与水平细杆E接触的一瞬间,小球a对地面的压力恰好为零,不计小球的大小,则下列说法正确的是
A.细线与水平细杆E接触一瞬间,小球b加速度大小不变
B.细线与水平细杆E接触一瞬间,小球b速度大小不变
C.小球a与小球b的质量之比为5:1
D.将D、E细杆向右平移相同的一小段距离再固定,由静止释放小球b,细 线与E相碰的一瞬间,小球a会离开地面
【答案】BCD
【解析】
AB.细线与水平细杆E接触的一瞬间,小球b速度不会发生突变,因此小球b速度大小不变,由于做圆周运动的半径减小,由![]() 可知,小球b加速度增大。故A错误,B正确。
可知,小球b加速度增大。故A错误,B正确。
小球b运动到最低点时,设速度为v,根据机械能守恒定律可知,![]() ,
,![]() ,C.细线与E相碰的一瞬间有:
,C.细线与E相碰的一瞬间有: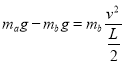 , 因此有:
, 因此有:
![]()
故C正确。
D.将D、E细杆向右平移相同的一小段距离再固定,设小球b开始做圆周运动的半径为L',与杆E相碰时的速度大小![]() ,设相碰的一.瞬间细线的拉力为F' ,则
,设相碰的一.瞬间细线的拉力为F' ,则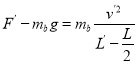 ,求得:
,求得:
![]()
因此细线与E相碰的一瞬间,小球a会离开地面。故D正确。

练习册系列答案
相关题目