题目内容
(1)一列简谐横波沿直线由a向b传播,相距10.5m的a、b两处的质点振动图象如图1所示中a、b所示,则
A.该波的振幅可能是20cm
B.该波的波长可能是8.4m
C.该波的波速可能是10.5m/s
D.该波由a传到b可能历时7s
(2)如图2所示是一种折射率n=1.5的棱镜,现有一束光线沿MN的方向射到棱镜的AB界面上,入射角的正弦值为sin i=0.75.求:
①光在棱镜中传播的速率;
②通过计算说明此束光线射出棱镜后的方向并画出光路图(不考虑返回到AB面上的光线).

D
D
A.该波的振幅可能是20cm
B.该波的波长可能是8.4m
C.该波的波速可能是10.5m/s
D.该波由a传到b可能历时7s
(2)如图2所示是一种折射率n=1.5的棱镜,现有一束光线沿MN的方向射到棱镜的AB界面上,入射角的正弦值为sin i=0.75.求:
①光在棱镜中传播的速率;
②通过计算说明此束光线射出棱镜后的方向并画出光路图(不考虑返回到AB面上的光线).

分析:(1)由振动图象可知波的振幅及周期;由图象得出同一时刻两质点的位置及振动方向,则可得出ab间可能含有的波长数,则可得出波长的表达式,波速公式可得出波速的可能值;则可知该波从a传播到b点可能经历的时间.
(2)①根据v=
求出光在棱镜中传播的速率;
②根据折射定律求出光线进入棱镜后折射角,由几何知识求出光线射到BC面上的入射角,由临界角大小,分析能否发生全反射,再作出光路图,确定光线射出棱镜后的方向.
(2)①根据v=
| c |
| n |
②根据折射定律求出光线进入棱镜后折射角,由几何知识求出光线射到BC面上的入射角,由临界角大小,分析能否发生全反射,再作出光路图,确定光线射出棱镜后的方向.
解答: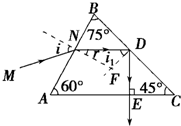 解:(1)A、由图可知,波的周期为4s,振幅为10cm,故A错误;
解:(1)A、由图可知,波的周期为4s,振幅为10cm,故A错误;
B、由图可知,在0时刻a在负向最大位置处,b在平衡位置向正方向运动,而波由a向b传播,则ab间距离与波长关系为:
xab=(n+
)λ,得,λ=
=
=
m(n=0,1,2,3…),因n是整数,λ不可能等于8.4m,故B错误;
C、由v=
可知,v=
m/s=
m/s(n=0、1、2…),n是整数,v不可能等于10.5m/s,故C错误;
D、由a到b需要的时间t=
=
s=(4n+3)s,当n=1时,t=7s,故D正确;
故选D.
(2)①光在棱镜中传播的速率:v=
=
=2×108m/s
②设光线进入棱镜后的折射角为r.
由n=
得,i=arcsin0.75,
代入解得:r=30°
在△NBD中,∠BND=60°,∠BDN=45°,光线射到BC界面时的入射角:i1=90°-∠BDN=45°
由sinC=
=
=
得:C=arcsin0.67
而i1=arcsin0.71
即:i1>C,故在BC界发生全反射.
根据几何知识得知,光线沿DE方向射出棱镜后的方向与AC边垂直,光路图如图所示.
故答案为:(1)D;(2)①光在棱镜中传播的速率是2×108m/s.②光线沿DE方向射出棱镜后的方向与AC边垂直,光路图如图所示.
 解:(1)A、由图可知,波的周期为4s,振幅为10cm,故A错误;
解:(1)A、由图可知,波的周期为4s,振幅为10cm,故A错误;B、由图可知,在0时刻a在负向最大位置处,b在平衡位置向正方向运动,而波由a向b传播,则ab间距离与波长关系为:
xab=(n+
| 3 |
| 4 |
| 4xab |
| 4n+3 |
| 4×10.5 |
| 4n+3 |
| 42 |
| 4n+3 |
C、由v=
| λ |
| T |
| ||
| 4 |
| 10.5 |
| 4n+3 |
D、由a到b需要的时间t=
| xab |
| v |
| 10.5 | ||
|
故选D.
(2)①光在棱镜中传播的速率:v=
| c |
| n |
| 3×108 |
| 1.5 |
②设光线进入棱镜后的折射角为r.
由n=
| sini |
| sinr |
代入解得:r=30°
在△NBD中,∠BND=60°,∠BDN=45°,光线射到BC界面时的入射角:i1=90°-∠BDN=45°
由sinC=
| 1 |
| n |
| 1 |
| 1.5 |
| 2 |
| 3 |
而i1=arcsin0.71
即:i1>C,故在BC界发生全反射.
根据几何知识得知,光线沿DE方向射出棱镜后的方向与AC边垂直,光路图如图所示.
故答案为:(1)D;(2)①光在棱镜中传播的速率是2×108m/s.②光线沿DE方向射出棱镜后的方向与AC边垂直,光路图如图所示.
点评:第1小题考查波的传播中的空间上的多解性,要注意ab间可能具有的波长个数,同时在确定两点之间的距离时,要找同一时刻时两点的位置及振动方向.
第2小题要根据折射定律和几何知识,通过计算来研究光路,当光从光密进入光疏介质时要考虑能否发生全反射.
第2小题要根据折射定律和几何知识,通过计算来研究光路,当光从光密进入光疏介质时要考虑能否发生全反射.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 物理 选修3-4
物理 选修3-4 (2009?枣庄一模)(1)一列简谐横波沿x轴传播,图甲是忙3s时的波形图,图乙是波上x=2cm处质点的振动图线.则该波的速度为
(2009?枣庄一模)(1)一列简谐横波沿x轴传播,图甲是忙3s时的波形图,图乙是波上x=2cm处质点的振动图线.则该波的速度为