题目内容
3. 我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆的近月点B处与空间站C对接.已知空间站绕月轨道的半径为r,周期为T,引力常量为G,月球的半径为R.下列说法正确的是( )
我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆的近月点B处与空间站C对接.已知空间站绕月轨道的半径为r,周期为T,引力常量为G,月球的半径为R.下列说法正确的是( )| A. | 航天飞机由椭圆轨道进入空间站轨道时必须减速 | |
| B. | 航天飞机在飞向B过程中月球引力做负功,动能减少 | |
| C. | 月球的质量为M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | |
| D. | 月球的第一宇宙速度为v=$\frac{2πr}{T}$ |
分析 要使航天飞机在椭圆轨道的近月点B处与空间站C对接,必须在接近B点时减速.根据开普勒定律可知,航天飞机向近月点运动时速度越来越大.月球对航天飞机的万有引力提供其向心力,由牛顿第二定律求出月球的质量M.月球的第一宇宙速度大于$v=\frac{2πr}{T}$.
解答 解:A、要使航天飞机在椭圆轨道的近月点B处与空间站C对接,必须在接近B点时减速.否则航天飞机将继续做椭圆运动.故A正确.
B、根据开普勒定律可知,航天飞机向近月点B运动时速度越来越大.月球引力做正功,故B错误.
C、设空间站的质量为m,由$\frac{GMm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$得,$M=\frac{{4{π^2}{r^3}}}{{G{T^2}}}$.故C正确.
D、空间站绕月圆轨道的半径为r,周期为T,其运行速度为$v=\frac{2πr}{T}$,其速度小于月球的第一宇宙速度,所以月球的第一宇宙速度大于$v=\frac{2πr}{T}$.故D错误.
故选:AC
点评 本题是开普勒定律与牛顿第二定律的综合应用,对于空间站的运动,关键抓住由月球的万有引力提供向心力,要注意知道空间站的半径与周期,求出的不是空间站的质量,而是月球的质量.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
8.一物体做匀变速直线运动,某时刻速度的大小为4m/s,1s后速度的大小变为10m/s.在这1s内物体( )
| A. | 位移的大小可能小于4m | B. | 位移的大小不可能大于10m | ||
| C. | 加速度的大小可能小于4m/s2 | D. | 加速度的大小可能大于10m/s2 |
15.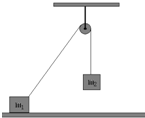 如图所示,质量分别为m1和m2的两个物体系在一根通过光滑轻滑轮的轻绳两端,m1放在水平地板上,m2被悬在空中,若将m1沿水平地板向右缓慢移动少许后,m1仍静止,则( )
如图所示,质量分别为m1和m2的两个物体系在一根通过光滑轻滑轮的轻绳两端,m1放在水平地板上,m2被悬在空中,若将m1沿水平地板向右缓慢移动少许后,m1仍静止,则( )
 如图所示,质量分别为m1和m2的两个物体系在一根通过光滑轻滑轮的轻绳两端,m1放在水平地板上,m2被悬在空中,若将m1沿水平地板向右缓慢移动少许后,m1仍静止,则( )
如图所示,质量分别为m1和m2的两个物体系在一根通过光滑轻滑轮的轻绳两端,m1放在水平地板上,m2被悬在空中,若将m1沿水平地板向右缓慢移动少许后,m1仍静止,则( )| A. | 绳子对m1的拉力变大 | B. | 滑轮轴所受的压力变大 | ||
| C. | m1对地面压力变大 | D. | m1所受的摩擦力变大 |
12.弹簧振子做简谐运动时,从振子经过某一位置P开始计时,则( )
| A. | 当振子再次与零时刻的速度相同时,经过的时间一定是一个周期 | |
| B. | 当振子再次经过P时,经过的时间一定是半周期 | |
| C. | 当振子的加速度再次与零时刻的加速度相同时,一定又到达位置P | |
| D. | 一定还有另一个位置跟位置P有相同的位移 |
13.关于太阳系中各行星的运动,开普勒指出:所有行星的轨道的半长轴的三次方与公转周期的二次方的比值都相等,即$\frac{{R}^{2}}{{T}^{2}}$=k,那么k的大小与下列哪些量有关( )
| A. | 行星的质量 | B. | 行星的运行速率 | ||
| C. | 行星与太阳的距离 | D. | 太阳的质量 |
 在“利用单摆测重力加速度”的实验中,为了准确的测出当地重力加速度值,
在“利用单摆测重力加速度”的实验中,为了准确的测出当地重力加速度值, 用双缝干涉测光的波长.
用双缝干涉测光的波长.