题目内容
 如图所示,一物体从A点沿光滑面AB与AC分别滑到同一水平面上的B点与C点,则下列说法中正确的是( )
如图所示,一物体从A点沿光滑面AB与AC分别滑到同一水平面上的B点与C点,则下列说法中正确的是( )分析:由于斜面光滑,由动能定理可以判定到底端的速度和动能,判定AB
对物体受力分析,求得加速度,然后列位移时间关系式计算时间,可判定CD
对物体受力分析,求得加速度,然后列位移时间关系式计算时间,可判定CD
解答:解:AB、斜面光滑,做功的只有重力,由于从同一位移下滑达到同一平面,故重力做功相同,由动能定理知,动能变化相同,故到底端的动能相同,但是由于速度方向不一样,故速度不相同.故A错误,B正确
物体沿斜面向下的合力为:F=mgsinθ,故其加速度为:a=
=gsinθ,位移为:x=
,由位移时间关系:x=
at2
得:
=
×gsinθ×t2
解得:t=
沿AB的θ角小,故沿AB的运动时间长.故C错误,D正确
故选BD
物体沿斜面向下的合力为:F=mgsinθ,故其加速度为:a=
| mgsinθ |
| m |
| h |
| sinθ |
| 1 |
| 2 |
得:
| h |
| sinθ |
| 1 |
| 2 |
解得:t=
|
沿AB的θ角小,故沿AB的运动时间长.故C错误,D正确
故选BD
点评:本题的一点小技巧就是用动能定理,或机械能守恒来解决AB两个选项,而不是用运动学来解,运动也能解,但是要麻烦一些.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
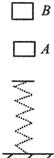 如图所示,一物体从A处下落然后压缩弹簧至最低点,在此过程中最大加速度为a1,动能最大时的弹性势能为E1;若该物体从B处下落,最大加速度为a2,动能最大时的弹性势能为E2,不计空气阻力,则有( )
如图所示,一物体从A处下落然后压缩弹簧至最低点,在此过程中最大加速度为a1,动能最大时的弹性势能为E1;若该物体从B处下落,最大加速度为a2,动能最大时的弹性势能为E2,不计空气阻力,则有( )| A、a1=a2 E1<E2 | B、a1<a2 E1<E2 | C、a1<a2 E1=E2 | D、a1=a2 E1=E2 |
 如图所示,一物体从A处下落然后压缩弹簧至最低点,在此过程中最大加速度为a1,动能最大时的弹性势能为E1;若该物体从B处下落,最大加速度为a2,动能最大时的弹性势能为E2,不计空气阻力,则有( )
如图所示,一物体从A处下落然后压缩弹簧至最低点,在此过程中最大加速度为a1,动能最大时的弹性势能为E1;若该物体从B处下落,最大加速度为a2,动能最大时的弹性势能为E2,不计空气阻力,则有( ) 如图所示,一物体从A点沿光滑面AB与AC分别滑到同一水平面上的B点与C点,则下列说法中正确的是( )
如图所示,一物体从A点沿光滑面AB与AC分别滑到同一水平面上的B点与C点,则下列说法中正确的是( ) 如图所示,一物体从A点出发以初速度v0冲上光滑斜面AB,并能沿斜面升高到h0不考虑空气阻力,说法中正确的是( )
如图所示,一物体从A点出发以初速度v0冲上光滑斜面AB,并能沿斜面升高到h0不考虑空气阻力,说法中正确的是( )