��Ŀ����
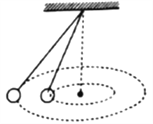
����Ŀ���ڹ⻬��ˮƽ�����Ͼ�ֹ��һ����M=0.4kg�ı�ľ�壬һ������m=0.2kg��ľ�飨����Ϊ�ʵ㣩��v0=4m/s���ٶȣ���ľ����˻��ϣ�һ��ʱ����ִ�ľ���ϻ��£�����ľ�黬��ʱ�Ļ�е����ʧ��������������ֱ������ǰ�˶�����ľ����ľ��ոշ��뿪ʼ��ʱ����ʱ��t=3.0s �� ������֮��ľ���������s=3m �� ��֪ľ����ľ��Ķ�Ħ��������=0.4����ľ��ij��ȣ�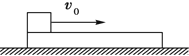
���𰸡���ľ����ľ�������ٶȷֱ�Ϊv1��v2 �� �涨ľ��ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵ�
mv0=mv1+Mv2
��v1��v2=s/t
���v1=2m/s �� v2=1m/s
�ɹ��ܹ�ϵ��
��mgd= ![]() mv02��
mv02�� ![]() mv12��
mv12�� ![]() Mv22
Mv22
�������ݽ�ã�
d=1.25m
��������ľ���ľ��ϵͳ��ˮƽ�����������������غ㣬���ݶ����غ㶨�ɺ���֪������ʽ�����������˲����Ե��ٶȣ�Ȼ����ݹ��ܹ�ϵ��ʽ���������ľ��ij��ȣ�
�����㾫�������ն����غ㶨���ǽ����ĸ�������Ҫ֪�������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�����Ŀ��Ҫ��Ħ�г��ɾ�ֹ��ʼ�ھ����̵�ʱ��������һ��ֱ����Ȼ��ʻ��һ�ΰ�Բ�ε�����������������ʻʱ���ٲ���̫�죬�������������ö�ƫ����������Ħ�г���ֱ������ʻ���õ����ʱ�䣬�й����ݼ�����ijͬѧ��������ģ�ҪʹĦ�г�����ʱ����̣�Ӧ���ɾ�ֹ���ٵ�����ٶ�v1=40m/s��Ȼ���ټ��ٵ�v2=20m/s��t1= ![]() =����t2=
=����t2= ![]() =����t=t1+t2=��
=����t=t1+t2=��
����Ϊ��λͬѧ�Ľⷨ�Ƿ������������������ɼ��㣻������������˵�����ɣ��������Լ��ķ��������ȷ�����
�������ٶ�a1 | 4m/s2 |
�ƶ����ٶ�a2 | 8m/s2 |
ֱ������ٶ�v1 | 40m/s |
�������ٶ�v2 | 20m/s |
ֱ������x | 167m |