题目内容
 如图所示.有一根长为2L的轻质细线,它的两端分别固定在一根长为L的竖直转轴AB上,线上套着一个可以自由移动的小环.当转轴转动时,小环正好以B点为圆心,在水平面内做匀速圆周运动.求:
如图所示.有一根长为2L的轻质细线,它的两端分别固定在一根长为L的竖直转轴AB上,线上套着一个可以自由移动的小环.当转轴转动时,小环正好以B点为圆心,在水平面内做匀速圆周运动.求:(1)线的拉力;
(2)小环的线速度.
分析:小环以B为圆心在水平面内作匀速圆周运动时,由重力、两个细线的拉力的合力提供向心力.根据几何知识,求出小环圆周运动的半径,由牛顿第二定律求解线的张力和小环的线速度.
解答:解:(1)设小球做匀速圆周运动的半径为r,则线长和半径之间的关系为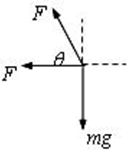 :
:
(2L-r)2=r2+L2
解得:r=0.75L.
则斜线与水平方向的夹角为:θ=53°
对小球受力分析如图所示,由牛顿第二定律可得:
F+Fcosθ=
Fsinθ=mg
联立两式,解得:
F=1.25mg,v=
答:(1)线的张力为1.25mg.
(2)小环的线速度是v=
.
 :
:(2L-r)2=r2+L2
解得:r=0.75L.
则斜线与水平方向的夹角为:θ=53°
对小球受力分析如图所示,由牛顿第二定律可得:
F+Fcosθ=
| mv2 |
| r |
Fsinθ=mg
联立两式,解得:
F=1.25mg,v=
| 1.5gL |
答:(1)线的张力为1.25mg.
(2)小环的线速度是v=
| 1.5gL |
点评:本题是圆锥摆类型的问题,在分析小球受力时,不能将水平细线的拉力漏掉.中等难度.

练习册系列答案
相关题目
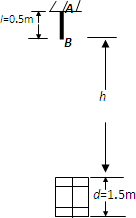
 如图所示,有一根长为l=0.5m的木棍AB,悬挂在某房顶上,它自由下落时经过一高为d=1.5m的窗口,通过窗口所用的时间为0.2s,求木棍B端离窗口上沿的距离h?(不计空气阻力,取g=10m/s2)
如图所示,有一根长为l=0.5m的木棍AB,悬挂在某房顶上,它自由下落时经过一高为d=1.5m的窗口,通过窗口所用的时间为0.2s,求木棍B端离窗口上沿的距离h?(不计空气阻力,取g=10m/s2) 如图所示,有一根长为2L的轻质细线,它的两端固定在一根长为L的竖直转轴AB上,线上套一个可以自由移动的质量为m的小球。当转轴转动时,小球正好以B为圆心,在水平面内做匀速圆周运动。求细线的张力和小球的线速度。
如图所示,有一根长为2L的轻质细线,它的两端固定在一根长为L的竖直转轴AB上,线上套一个可以自由移动的质量为m的小球。当转轴转动时,小球正好以B为圆心,在水平面内做匀速圆周运动。求细线的张力和小球的线速度。