题目内容
 水平面上有两个小球A和B,B的质量是A的2倍.小球A以速度v0向右运动,与静止的小球B发生碰撞,碰撞前后两球的运动都在一条直线上.若碰撞后A球的速度大小为
水平面上有两个小球A和B,B的质量是A的2倍.小球A以速度v0向右运动,与静止的小球B发生碰撞,碰撞前后两球的运动都在一条直线上.若碰撞后A球的速度大小为 | 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
向左
向左
.分析:两球碰撞过程,系统所受的合外力为零,根据动量守恒定律即可求解,注意碰撞后A的速度不能比B的速度大.
解答:解:碰撞前后,根据动量守恒定律得:
m1v0+0=m1v′1+m2v2
其中m2=2m1
碰撞后A球的速度大小为
v0,有两种情况,即v′1=
v0或v′1=-
v0
当v′1=
v0时,解得v2=
v0
必定还要发生碰撞,不符合实际
所以v′1=-
v0
解得v2=
v0,所以碰前A球速度的方向向左
故答案为:
v0,向左
m1v0+0=m1v′1+m2v2
其中m2=2m1
碰撞后A球的速度大小为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当v′1=
| 1 |
| 2 |
| 1 |
| 4 |
必定还要发生碰撞,不符合实际
所以v′1=-
| 1 |
| 2 |
解得v2=
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:碰撞最基本的规律是系统的动量守恒,要熟悉并能熟练应用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图所示,在光滑水平面上有两个小球A和B(可视为质点),质量mA=4kg,mB=2.0kg,球B静止在M点,球A在水平面上从很远处沿两球的中心连线以一个初速度向着B球运动.若已知在两球相距L>18m时,两球之间无相互作用力;在两球相距L≤18m时,它们之间存在着相互作用且大小恒定的斥力F.在运动过程中两球相距最近时的距离为d=6m,此时球A的瞬时速度是4m/s.求:
如图所示,在光滑水平面上有两个小球A和B(可视为质点),质量mA=4kg,mB=2.0kg,球B静止在M点,球A在水平面上从很远处沿两球的中心连线以一个初速度向着B球运动.若已知在两球相距L>18m时,两球之间无相互作用力;在两球相距L≤18m时,它们之间存在着相互作用且大小恒定的斥力F.在运动过程中两球相距最近时的距离为d=6m,此时球A的瞬时速度是4m/s.求: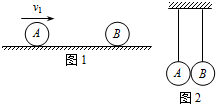 (1)如图1所示,光滑水平面上有两个小球A、B,A球以速度v1与原来静止的B球发生正碰,且碰撞过程中无机械能损失.设A球的质量为m1,B球的质量为m2.
(1)如图1所示,光滑水平面上有两个小球A、B,A球以速度v1与原来静止的B球发生正碰,且碰撞过程中无机械能损失.设A球的质量为m1,B球的质量为m2.
 ,则碰撞后小球B的速度大小为 ;小球A碰撞后的运动方向为 .
,则碰撞后小球B的速度大小为 ;小球A碰撞后的运动方向为 .