题目内容
【题目】如图,固定在水平地面上的一个粗糙斜面长L=4m,倾角θ=37°。一个质量为10kg的物体在F=200N的水平推力作用下,从斜面底端由静止开始沿斜面向上运动,经过2s到达斜面顶端。
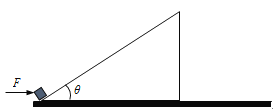
(1)求物体沿斜面运动时的加速度大小;
(2)求物体与斜面间的动摩擦因数大小;
(3)若物体运动到斜面顶端时恰好撤去推力F,求物体落到水平地面前瞬间的速度大小。
(已知sin37°=0.6,cos37°=0.8,重力加速度为g取10m/s2)
【答案】(1)2m/s2(2)0.4(3)8m/s
【解析】
(1)物体在斜面上做匀加速直线运动,根据运动学规律有:
L=![]() at2
at2
得: a = ![]() =2m/s2
=2m/s2
(2)物体在斜面上运动时受到四个力作用,如图所示。
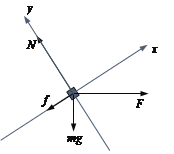
沿运动方向,根据牛顿第二定律有
Fcosθ-f-mgsinθ=ma
垂直于运动方向,合力为零:
Fsinθ+mgcosθ =N
f=μN
得![]()
代入已知数据得:μ=0.4
(3)物体离开斜面下落至地面前的过程中仅有重力做功,机械能守恒。设物体在斜面上运动的末速度为v1,落地前的速度大小为v2
根据匀加速直线运动的规律有 v1=at=2×2m/s=4 m/s
根据几何关系,斜面顶端到水平面的高度
h=Lsinθ =4×0.6m=2.4m
根据机械能守恒定律![]() mv12+mgh=
mv12+mgh=![]() mv22
mv22
得 ![]()
代入已知数据得:v2=8m/s。

练习册系列答案
相关题目