题目内容
如图甲所示，场强水平向左、大小E=3V/m的匀强电场中，有一倾角θ=37°的光滑绝缘斜面（足够大），垂直斜面方向有一磁场、磁感强度随时间的变化规律如图乙所示．在t=0时刻，质量m=4×10-3kg、电荷量q=10-2C的带负电的小球在O点获得一沿斜面向上的瞬时速度v=1m/s，求小球在t=0.32πs时间内运动的路程．（g=10N/kg，sin37°=0.6，cos37°=0.8）
分析：带电小球重力沿斜面方向上的分力与电场力沿斜面方向上的分力相等，则前半个周期内，小球做匀速圆周运动，后半个周期内小球做匀速直线运动，结合小球在磁场中运动的半径公式和周期公式，结合运动学公式求出小球在两个周期内的路程．
解答：解：如图甲所示，小球所受重力沿斜面向下的分力为
G1=mgsinθ=2.4×10-2N
电场力沿斜面向上的分力
F1=qEcosθ=2.4×10-2N
由于G1和F1相互平衡，小球将局限在斜面内运动．
在0≤t＜0.08πs内，小球在洛仑兹力作用下在斜面上做匀速圆周运动，运动半径、运动周期分别为R=
=0.08 m
T=
=0.16πs
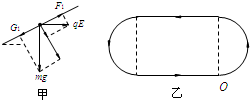
可见小球做圆周运动的周期与磁感强度变化的周期恰好相等．这就意味着在有磁场存在的半个周期内，小球做圆周运动，小球的运动路程为
y1=πR（或y1=
）
在没有磁场的半个周期内，小球做匀速直线运动，小球的运动路程为
y2=
小球在斜面内的运动轨迹如图乙所示．
小球在给定时间t=0.32πs=2T时间内，运动的路程为
y=2（y1+y2）=0.32πm．
答：小球在t=0.32πs时间内运动的路程为0.32πm．
G1=mgsinθ=2.4×10-2N
电场力沿斜面向上的分力
F1=qEcosθ=2.4×10-2N
由于G1和F1相互平衡，小球将局限在斜面内运动．
在0≤t＜0.08πs内，小球在洛仑兹力作用下在斜面上做匀速圆周运动，运动半径、运动周期分别为R=
| mv |
| qB |
T=
| 2πm |
| qB |
可见小球做圆周运动的周期与磁感强度变化的周期恰好相等．这就意味着在有磁场存在的半个周期内，小球做圆周运动，小球的运动路程为
y1=πR（或y1=
| vT |
| 2 |
在没有磁场的半个周期内，小球做匀速直线运动，小球的运动路程为
y2=
| vT |
| 2 |
小球在斜面内的运动轨迹如图乙所示．
小球在给定时间t=0.32πs=2T时间内，运动的路程为
y=2（y1+y2）=0.32πm．
答：小球在t=0.32πs时间内运动的路程为0.32πm．
点评：解决本题的关键理清在两个周期内的运动情况，结合运动学公式进行求解．
练习册系列答案
相关题目
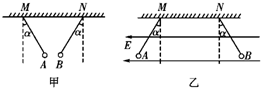质量都是m的两个完全相同、带等量异种电荷的小球A、B分别用长l的绝缘细线悬挂在同一水平面上相距为2l的M、N两点，平衡时小球A、B的位置如图甲所示，线与竖直方向夹角α=30°，当外加水平向左的匀强电场时，两小球平衡位置如图乙所示，线与竖直方向夹角也为α=30°，求：
两个等量同种电荷固定于光滑水平面上，其连线中垂线上有A、B、C三点，如图甲所示．一个电 量为2C，质量为1kg的小物块从C点静止释放，其运动的v～t图象如图乙所示，其中B点处为整 条图线切线斜率最大的位置（图中标出了该切线）．则下列说法正确的（ ）