题目内容
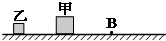
如图所示，水平面上从B点往左都是光滑的，从B点往右都是粗糙的．质量分别为M和m的两个小物块甲和乙（可视为质点），在光滑水平面上相距L以相同的速度同时开始向右运动，它们在进入粗糙区域后最后静止．若它们与粗糙水平面间的动摩擦因数相同，设静止后两物块间的距离为s，甲运动的总时间为t1、乙运动的总时间为t2，则以下说法中正确的是（ ）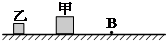
A．若M=m，则s=L
B．无论M、m取何值，总是s=0
C．若M=m，则t1=t2
D．无论M、m取何值，总是t1＜t2
【答案】分析：根据牛顿第二定律求出物块在B点右侧运动的加速度，根据匀变速直线运动的速度位移公式求出停止的位移与B点的距离，从而确定s的大小．根据速度时间公式求出从B点到停止所需的时间，从而比较出总时间的长短．
解答：解：物块在水平面上的加速度a=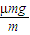
=μg，知两物块的加速度相等，因为经过B点的速度相等，根据
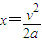，知停止距离B点的位移相等，则s=0．从B点运动到停止的时间t=
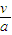，知两物块从B点到停止的时间相等，在B点左侧，因为乙的位移大于甲的位移，所以最终乙运动的总时间大于甲运动的总时间．故B、D正确，A、C错误．
故选BD．
点评：解决本题的关键知道加速度是联系前后的桥梁，根据加速度通过速度位移公式和速度时间公式进行求解．
解答：解：物块在水平面上的加速度a=
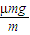=μg，知两物块的加速度相等，因为经过B点的速度相等，根据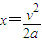，知停止距离B点的位移相等，则s=0．从B点运动到停止的时间t=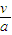，知两物块从B点到停止的时间相等，在B点左侧，因为乙的位移大于甲的位移，所以最终乙运动的总时间大于甲运动的总时间．故B、D正确，A、C错误．故选BD．
点评：解决本题的关键知道加速度是联系前后的桥梁，根据加速度通过速度位移公式和速度时间公式进行求解．
练习册系列答案
相关题目
如图所示，水平面上从B点往左都是光滑的，从B点往右都是粗糙的．质量为M和m的两个小物块（可视为质点），在光滑水平面上相距L以相同的速度向右运动，它们在进入粗糙区域后最后静止．若它们与粗糙水平面间的动摩擦因数相同，设静止后两物块间的距离为s，M运动的时间为t1、m运动的时间为t2，则以下说法正确的是（ ）
如图所示，水平面上从B点往左都是光滑的，从B点往右都是粗糙的。质量分别为M和m的两个小物块甲和乙（可视为质点），在光滑水平面上相距L以相同的速度同时开始向右运动，它们在进入粗糙区域后最后静止。若它们与粗糙水平面间的动摩擦因数相同，设静止后两物块间的距离为s，甲运动的总时间为t1、乙运动的总时间为t2，则以下说法中正确的是 ( )
| A．若M=m，则s=L |
| B．论M、m取何值，总是s=0 |
| C．若M=m，则t1= t2 |
| D．无论M、m取何值，总是t1< t2 |
