题目内容
3.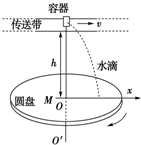 如图所示,M是水平放置的半径足够大的圆盘,绕过圆心O的竖直轴OO′匀速转动,规定经过O点且水平向右为x轴的正方向.在O点正上方距盘面高为h处有一个可间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时,后一滴水恰好开始下落,要使每一滴水在盘面上的落点都位于同一直线上,圆盘转动的角速度是nπ$\sqrt{\frac{g}{2h}}$(n=1,2,3,…).
如图所示,M是水平放置的半径足够大的圆盘,绕过圆心O的竖直轴OO′匀速转动,规定经过O点且水平向右为x轴的正方向.在O点正上方距盘面高为h处有一个可间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时,后一滴水恰好开始下落,要使每一滴水在盘面上的落点都位于同一直线上,圆盘转动的角速度是nπ$\sqrt{\frac{g}{2h}}$(n=1,2,3,…).
分析 水滴滴下后做平抛运动.根据平抛运动的高度求出运动的时间,结合圆周运动的周期性,可分析得出使每一滴水在盘面上的落点都位于一条直线上的条件.
解答 解:水滴在竖直方向做自由落体运动,有
h=$\frac{1}{2}g{{t}_{1}}^{2}$,得t1=$\sqrt{\frac{2h}{g}}$
要使每一滴水在圆盘面上的落点都位于同一条直线上,在相邻两滴水的下落时间内,圆盘转过的角度为nπ,所以角速度为
ω=$\frac{nπ}{{t}_{1}}$=nπ$\sqrt{\frac{g}{2h}}$(n=1,2,3,…)
故答案为:nπ$\sqrt{\frac{g}{2h}}$(n=1,2,3,…)
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道圆周运动的周期性,结合时间关系进行求解.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
13.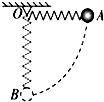 如图所示,一轻质弹簧固定于O点,另一端系一小球,将小球从与O点在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点B的过程中( )
如图所示,一轻质弹簧固定于O点,另一端系一小球,将小球从与O点在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点B的过程中( )
 如图所示,一轻质弹簧固定于O点,另一端系一小球,将小球从与O点在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点B的过程中( )
如图所示,一轻质弹簧固定于O点,另一端系一小球,将小球从与O点在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点B的过程中( )| A. | 小球的重力势能减少 | B. | 小球的重力势能增大 | ||
| C. | 小球的机械能不变 | D. | 小球的机械能增大 |
11.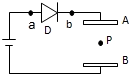 如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a.平行板电容器AB内部原有带电微粒P处于静止状态,当两极板A和B的间距稍增大一些后,微粒P的运动情况将是( )
如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a.平行板电容器AB内部原有带电微粒P处于静止状态,当两极板A和B的间距稍增大一些后,微粒P的运动情况将是( )
 如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a.平行板电容器AB内部原有带电微粒P处于静止状态,当两极板A和B的间距稍增大一些后,微粒P的运动情况将是( )
如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a.平行板电容器AB内部原有带电微粒P处于静止状态,当两极板A和B的间距稍增大一些后,微粒P的运动情况将是( )| A. | 向上运动 | B. | 向下运动 | C. | 仍静止不动 | D. | 无法判断 |
18.甲、乙两物体都做匀速圆周运动,其质量之比为2:1,转动半径之比为2:1,在相等时间里甲转过45°,乙转过60°,则它们所受外力的合力之比为( )
| A. | 4:1 | B. | 9:4 | C. | 3:2 | D. | 16:9 |
13.人造地球卫星在运行中,由于受到稀薄大气的阻力作用,其运动轨道半径会逐渐减小,在此过程中,以下说法中正确的是( )
| A. | 卫星的速率将增大 | B. | 卫星的周期将增大 | ||
| C. | 卫星的向心加速度将增大 | D. | 卫星的角速度将减小 |
 长为L质量分布均匀的绳子,对称地悬挂在轻小的定滑轮上,如图所示.轻轻地推动一下,让绳子滑下,那么当绳子离开滑轮的瞬间,绳子的速度为$\frac{\sqrt{gL}}{2}$.(重力加速度为g)
长为L质量分布均匀的绳子,对称地悬挂在轻小的定滑轮上,如图所示.轻轻地推动一下,让绳子滑下,那么当绳子离开滑轮的瞬间,绳子的速度为$\frac{\sqrt{gL}}{2}$.(重力加速度为g)