题目内容
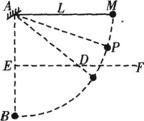
质量为m的小球由长为L的细线系住,细线的另一端固定在 A点,AB是过A的竖直线,且AB=L,E为AB的中点,过E作水平线 EF,在EF上某一位置钉一小钉D,如图所示.现将小球悬线拉至水平,然后由静止释放,不计线与钉碰撞时的机械能损失.
(1)若钉子在E点位置,则小球经过B点前后瞬间,绳子拉力分别为多少?
(2)若小球恰能绕钉子在竖直平面内做完整的圆周运动,求钉子D的位置离E点的距离x.
(3)保持小钉D的位置不变,让小球从图示的P点静止释放,当小球运动到最低点时,若细线刚好达到最大张力而断开,最后小球运动的轨迹经过B点.试求细线能承受的最大张力T.
解:(1)mgL=![]() mv2 1分 T1-mg=m
mv2 1分 T1-mg=m![]() 1分 T2-mg=m
1分 T2-mg=m![]() 1分
1分
∴T1=3mg 1分 T2=5mg 1分

(3)小球做圆周运动到达最低点时,速度设为v2 则
T-mg=m![]() ⑥ 2分
⑥ 2分
以后小球做平抛运动过B点,在水平方向有x=v2t ⑦ 1分
在竖直方向有: L/2-r=![]() gt2 ⑧ 2分
gt2 ⑧ 2分
由④⑤⑥⑦⑧式可得T=![]() mg 1分
mg 1分

练习册系列答案
相关题目
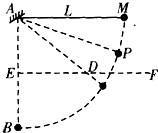 (2008?南通二模)质量为m的小球由长为L的细线系住,细线的另一端固定在 A点,AB是过A的竖直线,且AB=L,E为AB的中点,过E作水平线 EF,在EF上某一位置钉一小钉D,如图所示.现将小球悬线拉至水平,然后由静止释放,不计线与钉碰撞时的机械能损失.
(2008?南通二模)质量为m的小球由长为L的细线系住,细线的另一端固定在 A点,AB是过A的竖直线,且AB=L,E为AB的中点,过E作水平线 EF,在EF上某一位置钉一小钉D,如图所示.现将小球悬线拉至水平,然后由静止释放,不计线与钉碰撞时的机械能损失. 如图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为
如图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为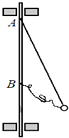 如图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为
如图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为