题目内容
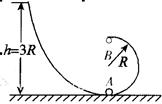
(10分)如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接,AB段长x=2.5m,半圆形轨道半径R=0.9m。质量m=0.10kg的小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,经B点时撤去力F,小滑块进入半圆形轨道,沿轨道恰好能通过最高点C,并从C点水平飞出。重力加速度g取10m/s2。求: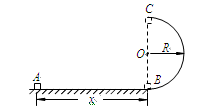
(1)滑块落地点与B点的水平距离;
(2)滑块刚进入半圆形轨道时,在B点对轨道压力的大小;
(3)拉力F的大小。
(1)1.8m;(2)6N;(3)0.9N。
解析试题解析:(1)由于滑块C恰好能通过C点,由牛顿第二定律可得:
mg=m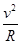
所以滑块从C点抛出的速度为v= =3m/s;
=3m/s;
由于滑块下落的时间t=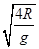 =0.6s;故滑块落地点与B点的水平距离x=vt=3×0.6m=1.8m;
=0.6s;故滑块落地点与B点的水平距离x=vt=3×0.6m=1.8m;
(2)滑块从B到C,遵循机械能守恒定律,则 mvB2=
mvB2= mv2+mg×2R,
mv2+mg×2R,
滑块在B点,应用牛顿第二定律可得:FB-mg=m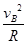
联立以上两式,解之得:FB=6N,根据力的相互性,故在B点滑块对轨道压力的大小为6N。
(3)滑块在经过AB段时,根据动能定理得:Fx= mvB2,故拉力F=0.9N。
mvB2,故拉力F=0.9N。
考点:圆周运动,牛顿第二定律,机械能守恒定律。

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
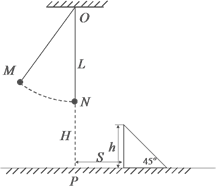
如右图所示,质量为m的小球,用长为l的细线挂在O点,在O点正下方 处有一光滑的钉子
处有一光滑的钉子 ,把小球拉到与钉子
,把小球拉到与钉子 在同一水平的位置,摆线被钉子拦住且张紧,现将小球由静止释放,当小球第一次通过最低点P时( )
在同一水平的位置,摆线被钉子拦住且张紧,现将小球由静止释放,当小球第一次通过最低点P时( )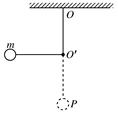
| A.小球的运动速度突然减小 |
| B.小球的角速度突然增大 |
| C.小球的向心加速度突然减小 |
| D.悬线的拉力突然增大 |


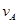 、
、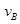 ;
;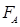 、
、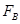 大小;
大小;