题目内容
10. 如图,金属杆MN放在完全相同的导体制成的金属框abcd上,并接触良好.沿线框bc边建立x轴,以b为坐标原点.矩形框ad边长2L,ab边长为L,导体单位长度的电阻为R0,磁感应强度为B的匀强磁场与框架平面垂直.现对MN杆施加沿x轴正方向的拉力,使之从框架左端开始,以速度v向右匀速运动,不计一切摩擦,求:
如图,金属杆MN放在完全相同的导体制成的金属框abcd上,并接触良好.沿线框bc边建立x轴,以b为坐标原点.矩形框ad边长2L,ab边长为L,导体单位长度的电阻为R0,磁感应强度为B的匀强磁场与框架平面垂直.现对MN杆施加沿x轴正方向的拉力,使之从框架左端开始,以速度v向右匀速运动,不计一切摩擦,求:(1)在MN杆运动的过程中,通过杆的电流与坐标x的关系.
(2)作用在MN杆上的外力的最大值与最小值之比.
分析 (1)先根据电路的结构求回路总电阻与x的关系,再由E=BLv、欧姆定律求解电流与x的关系.
(2)当MN中电流最小时拉力最小,当电流最大时拉力最大.由上题结果求出最大和最小电流,再由安培力公式和平衡条件求解.
解答 解:(1)设导体杆MN的坐标为x,则杆左侧电阻R1和右侧电阻R2分别为 R1=(L+2x)R0,R2=[L+2(2L-x)]R0,
回路总电阻R=$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$+LR0=$\frac{11{L}^{2}+8Lx-4{x}^{2}}{6L}$R0
杆运动产生的感应电动势 E=BLv
杆MN中电流 I=$\frac{E}{R}$=$\frac{6B{L}^{2}v}{(11{L}^{2}+8Lx-4{x}^{2}){R}_{0}}$
(2)当x=L时,R有最大值,I有最小值,拉力F也有最小值.
I的最小值为 Imin=$\frac{6B{L}^{2}v}{(11{L}^{2}+8{L}^{2}-4{L}^{2}){R}_{0}}$=$\frac{6Bv}{15{R}_{0}}$=$\frac{2Bv}{3{R}_{0}}$
F的最小值为 Fmin=BIminL=$\frac{2{B}^{2}Lv}{5{R}_{0}}$
当x=0或x=2L时,R有最小值,I有最大值.
I的最大值为 Imax=$\frac{6B{L}^{2}v}{11{L}^{2}{R}_{0}}$=$\frac{6Bv}{11{R}_{0}}$
拉力F也有最大值,最大值为 Fmax=BImaxL=$\frac{6{B}^{2}Lv}{11{R}_{0}}$
所以Fmax:Fmin=15:11
答:
(1)在MN杆运动的过程中,通过杆的电流与坐标x的关系是I=$\frac{6B{L}^{2}v}{(11{L}^{2}+8Lx-4{x}^{2}){R}_{0}}$..
(2)作用在MN杆上的外力的最大值与最小值之比是15:11.
点评 本题是电磁感应中电路问题,要理解并掌握电流与外电阻的关系,运用数学极值法分析.

 阅读快车系列答案
阅读快车系列答案| A. | 点电荷是一种物理模型,质子直接作为点电荷处理 | |
| B. | 电场强度反映了电场的力的性质,因此电场中某点的电场强度与试探电荷在该点所受的电场力成正比 | |
| C. | 电场中某点电场强度的方向与试探电荷在该点所受的静电力方向相同 | |
| D. | 库仑定律和万有引力定律的表达式相似,都是平方反比定律 |
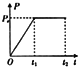 如图所示为某汽车启动时发动机功率P随时间t变化的图象,图中Pe为发动机的额定功率,若已知汽车的最大速度为vm,据此可知( )
如图所示为某汽车启动时发动机功率P随时间t变化的图象,图中Pe为发动机的额定功率,若已知汽车的最大速度为vm,据此可知( )| A. | 汽车匀速运动时受的阻力为$\frac{{P}_{e}}{2{v}_{m}}$ | |
| B. | 0-t1时间内发动机做的功为Pet1 | |
| C. | t1-t2时间内汽车做匀速运动 | |
| D. | 0-t2时间内发动机做的功为Pe(t2-$\frac{1}{2}$t1) |
| A. | 12:1 | B. | 6:1 | C. | 3:4 | D. | 2:3 |
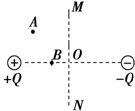 如图所示MN是两个等量异种点电荷连线的中垂线,O为两点电荷连线的中点,A、B在MN同侧且到+Q的距离相等,则下列说法正确的是( )
如图所示MN是两个等量异种点电荷连线的中垂线,O为两点电荷连线的中点,A、B在MN同侧且到+Q的距离相等,则下列说法正确的是( )| A. | A、B、O三点中A点的电场强度最大 | |
| B. | 将检验电荷+q从A点移动到B点,静电力做功为零 | |
| C. | 检验电荷+q在A点的电势能大于在B点的电势能 | |
| D. | 把电子从A点移动到MN上任何一点,电子的电势能都增加 |
| A. | 同一物体所受的静摩擦力一定比滑动摩擦力大 | |
| B. | 静摩擦力与压力成正比 | |
| C. | 最大静摩擦力与接触面之间的粗糙程度有关 | |
| D. | 滑动摩擦力与接触面之间的粗糙程度有关,压力一定时,接触面越粗糙,滑动摩擦力越大 |
 质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为s1和s2,如图所示.则这段时间内此人所做的功的大小等于( )
质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为s1和s2,如图所示.则这段时间内此人所做的功的大小等于( )| A. | Fs2 | B. | Fs1 | ||
| C. | $\frac{1}{2}$m2v22+$\frac{1}{2}$(m+m1)v12 | D. | $\frac{1}{2}$m2v22 |
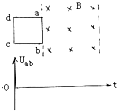 用匀质导线做的正方形线框abcd,边长为L,以恒定的速率v匀速通过一个宽度为2L的匀强磁场区,磁感应强度为B,磁场方向与线框平面垂直.t=0时,ab边与磁场的右边界重合,如图所示,试画出从t=0 到线框刚完全离开磁场时ab电势差Uab与t的关系图象.(在图上要标明坐标)
用匀质导线做的正方形线框abcd,边长为L,以恒定的速率v匀速通过一个宽度为2L的匀强磁场区,磁感应强度为B,磁场方向与线框平面垂直.t=0时,ab边与磁场的右边界重合,如图所示,试画出从t=0 到线框刚完全离开磁场时ab电势差Uab与t的关系图象.(在图上要标明坐标)