题目内容
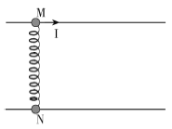
【题目】如图所示,两平行光滑杆水平放置,两相同的小球M、N分别套在两杆上,并由轻弹簧拴接,弹簧与杆垂直。已知两杆间距为0.4m,弹簧原长为0.5m,两球的质量均为0.2kg。现给M球一沿杆向右![]() 的瞬时冲量,关于之后的运动,以下说法正确的是( )
的瞬时冲量,关于之后的运动,以下说法正确的是( )
A.M球在开始的一段时间内做加速度增大的加速运动,直到达到运动中的最大速度
B.弹簧第一次达到0.6m时,M球的速度大小为3m/s
C.弹簧达到0.5m时,M球和N球总动能最大
D.弹簧达到最长时,M球的速度大小为1.5m/s
【答案】BCD
【解析】
A.在最开始时,弹簧处于压缩状态,当M球开始运动后,弹簧恢复原长,形变量逐渐减小,因此弹力逐渐减小,根据牛顿第二定律可知,加速度逐渐减小,即该过程M球做加速度逐渐减小的加速运动,故A错误;
B.设一开始弹簧的形变量为![]() ,当弹簧达到0.6m时形变量为
,当弹簧达到0.6m时形变量为![]() ,则有
,则有
![]()
![]()
M球在瞬间冲量作用后,获得动量,由动量定理可得
![]()
两球和弹簧组成的系统,合外力为零,根据动量守恒定律可得
![]()
当弹簧第一次达到0.6m时,根据能量守恒定律有
![]()
解得
![]()
即弹簧达到0.6m时,M球的速度大小为3m/s,故B正确;
C.根据能量守恒定律,该过程M球和N球的总动能与弹簧的弹性势能相互转化,当弹簧的弹性势能为0时,M球和N球的总动能达到最大。故C正确。
D.当两球速度第一次相等时,弹簧第一次达到最大伸长量,根据动量守恒定律可得
![]()
解得
![]()
即弹簧达到最长时,M球的速度大小为1.5m/s,故D正确。
故选BCD。

练习册系列答案
相关题目