题目内容
如图12所示，足够长的斜面倾角θ=37°，一物体以v0=12m/s的初速度，从斜面A点沿斜面向上运动，加速度大小为a=8.0m／s2．已知重力加速度g=10m/s2，sin 37°= 0.6，cos 37°=0.8．求：
（1）物体沿斜面上滑的最大距离s；
（2）物体与斜面间的动摩擦因数μ；
（3）物体沿斜面到达最高点后返回下滑至A点时的速度大小v．
（1）9m（2）0.25（3）8.5（m／s）
解析:
熟练掌握牛顿第二定律和匀加速直线运动规律是是求解此题的关键。另外就是对物体的受力和运动情景要分析准确、到位，计算过程中要倍加细心和严谨，问题即可得到解决。
（1）根据运动学公式 2as ＝ v 解得 s＝ ＝ ＝ 9m
（2）根据牛顿第二定律 mg sin 37°＋ μmg cos 37°＝ ma
解得 μ ＝ ＝ － tan 37°
＝ － ＝ 0.25
（3）设沿斜面下滑时的加速度为a′，根据牛顿第二定律
mg sin 37°－ μmg cos 37°＝ ma′
解得 a′＝ g sin 37°－ μg cos 37°
＝ g （sin 37°－ μ cos 37°）
＝10×（0.6－0.8×）＝ 4 （m／s2）
根据运动学公式 2a′s ＝ v2
解得 v＝ ＝ ＝6 ＝8.5（m／s）
练习册系列答案
相关题目
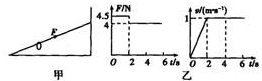如图甲所示，足够长的固定光滑细杆与地面成一定倾角，在杆上套有一个光滑小环，小环在沿杆方向的推力F作用下向上运动，推力F及小环速度v随时间变化规律如图乙所示，取重力加速度g=10m/s2．则以下判断正确的是（ ）| A、小环的质量是l kg | B、细杆与地面间的倾角是30° | C、前4s内小环机械能的增量是12.5J | D、前4s内拉力F的最大功率是4.25W |
P=I2R=
（其中R为回路总电阻）
