题目内容
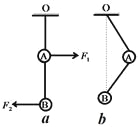
【题目】如图所示,在场强E=104 N/C的水平匀强电场中,有一根长L=15 cm的细线,一端固定在O点,另一端系一个质量m=3 g、电荷量q=2×10-6 C的带正电小球,当细线处于水平位置时,小球从静止开始释放,g取10 m/s2。求:
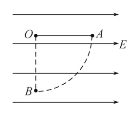
(1)小球到达最低点B的过程中重力势能、电势能分别变化了多少?
(2)小球到B点时速度为多大?绳子张力为多大?
(3)小球在摆动过程中何处速度最大?最大速度为多少?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)从A→B重力做正功,重力势能减少:ΔE=WG=mgL=4.5×10-3 J
从A→B电场力做负功,电势能增加:ΔEp=-WE=EqL=3×10-3 J
(2)从A→B由动能定理知: mgL-EqL=![]() mvB2
mvB2
代入数据得:vB=1 m/s
在B点由牛顿第二定律知:F=mg+m![]()
代入数据得:F=5×10-2 N。
(3)小球的速度最大的位置在平衡位置,设此位置细线与竖直方向的夹角为θ,则满足![]()
由动能定理得:mgLcosθ-qEL(1-sinθ)=![]() mv2-0,
mv2-0,
整理得:3cosθ-2(1-sinθ)=v2,
解得:![]()

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目